Data Generation and Neural Network Training for TMDs and Moiré Superlattices
Introduction to Neural Network Potentials
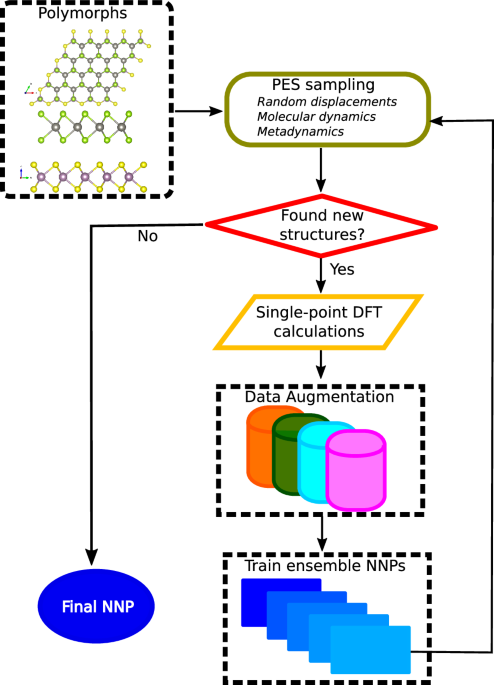
The concept of neural network potentials (NNPs) has gained significant traction as an efficient computational method to approximate the potential energy surfaces of materials, especially in the realm of few-layer transition metal dichalcogenides (TMDs) and moiré superlattices. The pursuit of accuracy that parallels density functional theory (DFT) necessitates a systematic approach that efficiently generates datasets. This article describes a detailed methodology based on an active learning strategy, enhancing the efficiency and accuracy of neural network training processes.
Active Learning in Dataset Generation
To develop an NNP reflecting DFT accuracy in energy and forces for few-layer TMDs, we initiate the process through a carefully structured dataset. The primary advantage of using small unit cells rather than twisted bilayer TMDs is the minimization of computational cost associated with DFT calculations. The training process begins with monolayer, homobilayer, and strained TMD bilayer heterostructures that exhibit both AA and AB stacking configurations. This yields a total of 35 distinct structures.
Sampling the Potential Energy Surface
For effective representation of the potential energy surface of layered TMDs, we explore various polymorphs through random atomic displacements. Each configuration generated is based on 500 atomic arrangements, where the displacements are selected from a Gaussian distribution with a fixed width of 0.05 Å. Using an ensemble of five NNPs, we execute molecular dynamics (MD) simulations across diverse temperatures and pressures, specifically designed to mitigate finite-size effects through the use of 3×3×1 supercells.
Molecular Dynamics and Active Learning Cycle
Our molecular dynamics simulations are conducted at various pressure and temperature combinations—specifically 0 and ±1 GPa, at 300 K and 800 K. For each scenario, configurations are gathered every 200 time steps, resulting in a vast array of 1000 snapshots per structural category. To enhance the active learning loop’s efficacy, we compute the ensemble root mean square deviation based on energies, retaining only those snapshots with significant ensemble errors (above 2.5 meV/atom) for further DFT calculations.
Metadynamics and Enhanced Sampling
To capture configurations beyond conventional AA and AB stacking that may not be accessed by unbiased MD simulations, we adopt metadynamics using collective variables. This strategic sampling focuses on interlayer distances between transition metals in different TMD monolayers, effectively illustrating the potential energy surface associated with slippage of one layer over another. This method, combined with the active learning cycle, leads to the generation of approximately 89,400 configurations.
Incorporating Substrate Interaction
Our dataset expansion includes TMD-hexagonal boron nitride (hBN) configurations in a two-step approach. Initially, we generate random configurations for monolayer TMDs supported on single-layer hBN, followed by additional configurations extracted from MD simulations at room temperature. Collectively, the final dataset encompasses around 92,600 unique structures, ensuring a well-rounded representation of the potential energy landscape.
Neural Network Potential Architecture
The construction of our NNP leverages modified Behler-Parrinello symmetry functions (BPSFs), which elegantly account for the multifaceted chemical environments within the systems analyzed. Utilizing PANNA software, we establish cutoffs of 8 Å for radial descriptors and 4 Å for angular descriptors, creating comprehensive input vectors for a fully connected neural network architecture. This includes two hidden layers of 64 nodes each, culminating in an output layer that predicts atomic energy.
Van der Waals Corrections
To enhance accuracy, particularly for systems dominated by van der Waals interactions, a correction term inspired by existing work is added to the NNP. This term, expressed in mathematical form, smoothly transitions to long-range interactions, thus accommodating the nuances of layered TMD interactions.
Model Training and Validation
The model training employs the Adam optimizer, optimizing for mean absolute error (MAE) in energy and force predictions. The achieved MAE demonstrates minimal differences between training and test sets, indicating robust transferability of the NNP. The energy and force correlations between DFT results and NNP predictions exhibit exceptional agreement, reflective of the NNP’s predictive capability.
Interlayer Binding and Sliding Energetics
One of the key validations of our NNP involves examining interlayer binding energy concerning the interlayer separation and sliding distance—critical parameters for analyzing TMD stability and behavior in moiré superlattices. Our experiments include systematic assessments of various configurations, benchmarked against DFT results, to ascertain model fidelity.
Vibrational Properties Declared
A thorough investigation into the vibrational properties of homobilayer TMDs further establishes the applicability of our NNP in modeling dynamical behavior. Accurate predictions of vibrational frequencies are essential for understanding thermal transport phenomena, laying the groundwork for future explorations and applications in nanostructured devices.
Toward Moiré Superlattices
The NNP’s adaptability extends to the realm of moiré superlattices, where its performance is meticulously assessed against large-angle twisted bilayer TMDs. By exploring atomic forces and spatial configurations across different stacking arrangements, we build confidence in the model’s ability to simulate larger, complex systems.
Future Directions
As research progresses into the interplay between atomic reconstructions and electronic structures, the developed NNP provides a robust foundation for delving into intricate systems such as twisted bilayer TMDs. The insights gained from the interaction of TMDs with substrates further elucidate the significance of mechanical constraints on material properties.
In summary, the deployment of a systematic active learning approach in conjunction with NNPs allows for an efficient and accurate representation of potential energy surfaces in TMDs and their heterostructures. The tools and methods discussed herein pave the way for deeper explorations into the unique properties of these two-dimensional materials.