Properties of Euclidean Convex Sets

Introduction to Convexity in Euclidean Spaces

In the realm of geometry, a set in Euclidean spaces is termed convex if the line segment connecting any two points within that set also lies entirely within it. This essential characteristic establishes the foundational understanding of convexity and applies a wide range of mathematical and real-world applications, from optimization to computer science.

Let’s formalize this understanding: a subset ( S \subset \mathbb{R}^D ) is defined as convex if for any two points ( \mathbf{x}, \mathbf{y} \in S ) and for every ( t \in [0, 1] ), the point ( \mathbf{y}(t) = t\mathbf{x} + (1 – t)\mathbf{y} ) also belongs to ( S ). This definition emphasizes the intrinsic connection between points in a convex set.

Key Properties of Euclidean Convex Sets

One important property derived from the definition is that the intersection of two convex sets is also convex. This means that if we have two convex sets ( A ) and ( B ), then their intersection ( A \cap B ) maintains the property of convexity.

Conversely, the union of convex sets does not necessarily preserve this property. For example, consider two distinct, non-overlapping convex shapes; their union would not be convex since a line segment drawn between points from different shapes would not remain within the combined area.

Transformations and Robustness

Euclidean convexity exhibits robustness under affine transformations, meaning that operations such as translation, scaling, and rotation do not alter the fundamental convex nature of a set. Such resilience is particularly useful in machine learning contexts, where latent space transformations in deep networks require stable geometric properties.

Relationship to Linear Classifiers

In another realm, convex sets closely relate to linear classifiers. A convex set can be expressed as the intersection of linear half-spaces. This brings about practical applications in machine learning, where linear decision boundaries often constitute convex regions in the feature space.

Geometric Structures Beyond Euclidean Spaces

While Euclidean spaces offer valuable insights, they are not the only geometric structures we encounter. In more complex settings, such as Riemannian manifolds, the concept of convexity must be redefined. In this setting, the shortest path between two points is represented by a geodesic, which can vary greatly in shape and uniqueness compared to Euclidean geodesics.

Defining Geodesic Convexity

In this context, a subset ( S ) in a manifold ( M ) can be termed geodesic convex if, for any two points ( \mathbf{x}, \mathbf{y} \in S ), there exists at least one geodesic connecting them that lies entirely within ( S ). This generalization of convexity helps us navigate through complex geometrical landscapes encountered in advanced data analysis and deep learning applications.

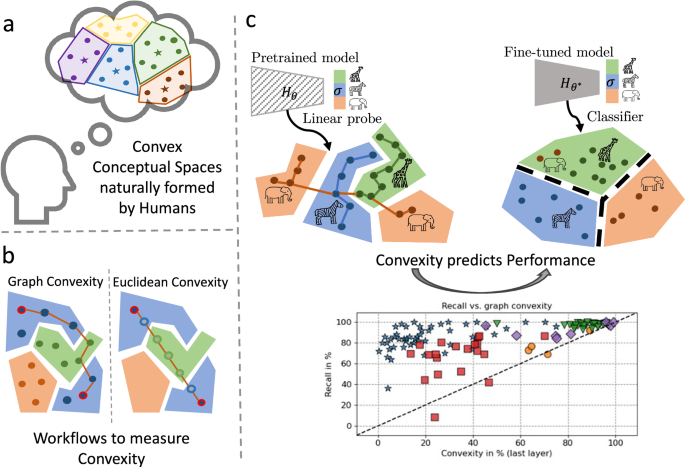
Graph Convexity

Beyond these geometric formulations, we can also derive a notion of graph convexity. In a graph ( (V, E) ), a subset ( A \subseteq V ) is considered convex if every pair ( x, y \in A ) is connected by a shortest path in the graph that entirely comprises nodes from ( A ). This enables us to explore connectivity in various data-driven contexts, reinforcing our understanding of structures within learned representations.

Neural Networks and their Convex Decision Regions

When it comes to neural networks, one of the pressing questions arises: Do we expect the decision regions of neural network representations to exhibit convexity?

Mechanisms Promoting Convexity

Several aspects of neural networks and their architectures inherently foster convexity:

1. Softmax Activation: This popular function in classification models tends to enforce convex boundaries in the activation layer. Essentially, the decision regions can be likened to those created by linear models, which are uniformly convex.

2. Transformer Architectures: Many modern neural networks, particularly transformers with attention mechanisms, utilize softmax. This influences the convexity in how attention is allocated across various dimensions of the data.

3. Activation Functions: Individual neurons with specific activation functions, like ReLU, can represent latent half-space detectors. In essence, the regions within these half-spaces are inherently convex, hinting at a structural inclination towards convexity in multilayer networks.

Exploration of Convexity During Training

Research indicates that fine-tuning neural networks continues to promote convexity, as seen in both Euclidean and graph-based convexity scores across different layers of the network. Insights gleaned from t-SNE plots reveal how clustered regions form during initial training and how they become more pronounced with subsequent fine-tuning.

Measuring Convexity: A Workflow

To quantify convexity, especially in neural networks, a structured approach can be deployed.

1. Graph Construction: Representations of data points are organized into a graph, where nodes symbolize the data points, and edges are defined based on the Euclidean distances between them.

2. Shortest Path Calculation: Using algorithms like Dijkstra’s, one can compute the shortest paths between nodes within the specified class. The endpoints’ connectivity allows for meaningful evaluations of convexity based on the paths’ lengths and distributions.

3. Performance Correlation: By plotting convexity measures against performance metrics such as accuracy, we can derive insights into how structural properties of the decision space correlate with the model’s effectiveness on given tasks.

Convexity in Various Domains

Convexity has been shown to be a salient feature across multiple domains, impacting both image and text processing tasks. The strong relationships discovered between convexity metrics in pretrained models and their performance in downstream applications underscore the importance of considering both Euclidean and graph convexity for better model selection and refinement strategies.

Neural networks, through their multifaceted architectures and the various forms of data they process, provide fertile ground for investigating convexity in mathematical representation. As we continue to delve into these structures, understanding convexity remains pivotal not only for the performance of these models but also for interpreting their decision-making processes in the complex, high-dimensional spaces they navigate.