Hybrid Machine Learning: Unraveling Complex Dynamical Systems

Introduction to Hybrid Machine Learning

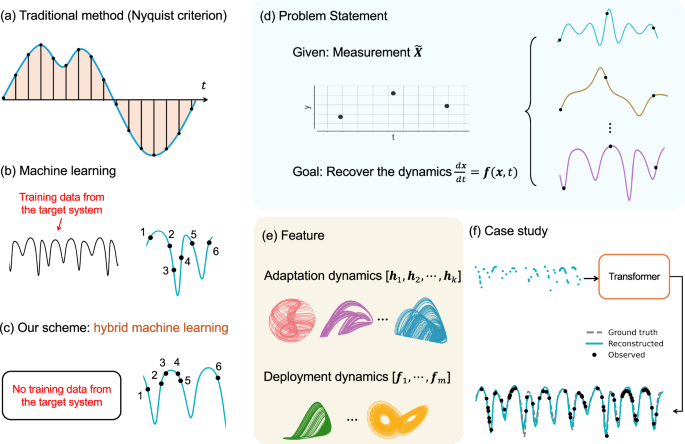
Hybrid machine learning leverages the strengths of different computational techniques to address complex nonlinear dynamical systems. These systems are often characterized by intricate behaviors that can be challenging to model accurately. At the core of this approach is the interplay between traditional dynamical mathematics and advanced machine learning methods, specifically designed to handle sparse observational data.

Understanding Nonlinear Dynamical Systems

A nonlinear dynamical system can be described mathematically as follows:

[
\frac{d{{\bf{x}}}(t)}{dt}={\bf{F}}({\bf{x}}(t),t),\quad t\in [0,T],
]

where ({\bf{x}}(t) \in \mathbb{R}^{D}) is the state vector in an (D)-dimensional space, and (\bf{F}) is the unknown velocity field governing the dynamics of the system. The behavior of this system over time is crucial for understanding the dynamical properties and long-term forecasts.

Observational Data Representation

To analyze these systems, we establish a data matrix ({\bf{X}} = ({\bf{x}}{0}, \ldots, {\bf{x}}{L_s})^{\top} \in \mathbb{R}^{L_s \times D}) containing uniformly sampled data points. Here, (L_s) represents the number of samples collected across the (D) dimensions.

When dealing with physical systems, the observational vector is often sparse, which is captured by the equation:

[
\tilde{{\bf{X}}} = {\bf{g}}_{\alpha}({\bf{X}})(1 + \sigma \cdot \Xi),
]

where (\tilde{{\bf{X}}} \in \mathbb{R}^{L_s \times D}) reflects the noisy observations of the true data measured with a certain level of uncertainty represented by (\sigma) and noise term (\Xi \sim \mathcal{N}(0,1)).

The Role of Machine Learning

The central goal of hybrid machine learning in this context is to approximate the system dynamics represented by (\bf{F}) through another function ({\bf{F}}^{\prime}(\cdot)) under the assumption that (\bf{F}) is Lipschitz continuous. This approximation aims to reconstruct the underlying dynamical behavior by filling the observational gaps, which is represented implicitly by the function:

[
\mathcal{F}(\tilde{{\bf{X}}}) = {\bf{X}}.
]

The effectiveness of this reconstruction relies significantly on carefully chosen neural network architectures.

Selecting the Right Neural Network

For reconstructing system dynamics efficiently, a neural network should encompass:

1. Dynamical Memory: It can capture long-range dependencies from the sparse datasets.
2. Flexibility: It can handle variable-length input sequences.

Transformers, initially developed for natural language processing, have emerged as a suitable architecture for this task. Their attention mechanisms, which allow the model to focus on different parts of the input sequence, provide significant advantages in time series analysis.

Transformer Architecture

The transformer processes the sparse observational data matrix through several layers, which include:

1. Linear Transformation: The input matrix is transformed through a linear fully-connected layer.

   [
   {\bf{X}}_p = \tilde{{\bf{X}}} {\bf{W}}_p + {\bf{W}}_b + {\bf{PE}},
   ]

   where ({\bf{PE}}) denotes positional encoding essential for retaining temporal order.

2. Self-Attention Mechanism: Each attention block computes attention scores, which determine the significance of various time steps.

3. Feed-Forward Layers: Each self-attention output passes through a series of feed-forward layers equipped with activation functions, enhancing the model’s representational capacity.

By stacking multiple blocks, the transformer learns representations that capture both local and global patterns in data.

Reservoir Computing: The Second Component

Alongside transformers, reservoir computing is introduced as a powerful tool for long-term forecasting or reconstructing the attractor of the target system. This method leverages the outputs from the transformer, effectively combining them to yield more stable and reliable predictions.

Machine Learning Loss Functions

To evaluate the performance of the hybrid machine learning framework, a composite loss function is minimized, including:

1. Mean Squared Error (MSE): Gauges the absolute error between the outputs and ground truth.

   [
   \mathcal{L}{\text{mse}} = \frac{1}{n} {\sum}{i=1}^n (y_i – \hat{y}_i)^2,
   ]

2. Smoothness Loss: Ensures the continuity of predictions, promoting smoother outcomes.

The complete loss function can be formulated as:

[
\mathcal{L} = \alpha1 \mathcal{L}{\text{mse}} + \alpha2 \mathcal{L}{\text{smooth}}.
]

Careful selection of hyperparameters is crucial to strike a balance between accuracy and smoothness, leading to more robust model performance.

Computational Settings

In practical applications, specifics matter. Time series data is generated through numerical integration, with initial states randomized. Data normalization and strategic sampling further refine the datasets. Various optimization techniques, including Bayesian optimization and random search, identify the optimal hyperparameters that enhance learning.

Prediction Stability Assessment

Stability in predictions is critical for the reliability of outcomes in machine learning models. Here, prediction stability is defined as the probability that the constructed model’s MSE remains below a certain threshold:

[
R_s({\text{MSE}}c) = \frac{1}{n} \sum{i=1}^n [\text{MSE} < \text{MSE}_c].
]

Assessing Deviation and Noise Implementation

In evaluating the model, deviation quantifies differences between predicted and actual trajectories. Two noise types—multiplicative and additive—are explored to examine their impacts on reconstruction accuracy.

This comprehensive examination of hybrid machine learning strategies advances our understanding and capability in addressing the intricacies of nonlinear dynamical systems, paving the way for applications across various scientific and engineering fields.