Evaluating U-235 Fission Cross Sections: Adaptive Resampling and HDF5 Framework

Introduction to U-235 Fission Cross Sections

In nuclear physics, understanding the behavior of isotopes under various conditions is crucial for applications ranging from nuclear energy generation to safety assessments. Among the key isotopes, Uranium-235 (U-235) plays a pivotal role, particularly in fission processes. The fission cross-section data provides insights into the likelihood of reactions occurring, significantly influencing reactor simulations and safety margins.

Methodology Overview

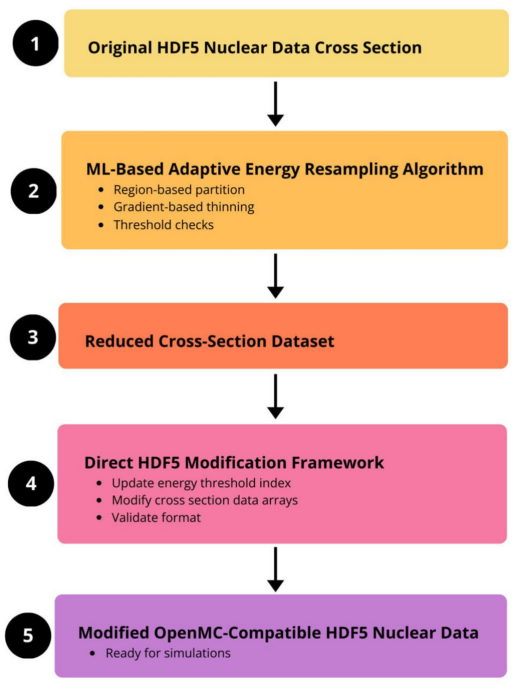
The present study aims to evaluate a novel adaptive resampling algorithm and a direct HDF5 modification framework for U-235 fission cross sections, specifically focusing on the neutron fission process (denoted as ((n,f))) under seven discrete temperatures: (0\,\text{K}), (250\,\text{K}), (294\,\text{K}), (600\,\text{K}), (900\,\text{K}), (1200\,\text{K}), and (2500\,\text{K}). The dataset utilized in the analysis was sourced from the ENDF/B-VII.1 library, which is a renowned database for nuclear data.

Original Dataset Sizes

The baseline dataset for each temperature contained the following number of data points:

• (0\,\text{K}): 242,593 points
• (250\,\text{K}): 80,882 points
• (294\,\text{K}): 76,514 points
• (600\,\text{K}): 60,631 points
• (900\,\text{K}): 53,930 points
• (1200\,\text{K}): 50,104 points
• (2500\,\text{K}): 43,405 points

The Adaptive Resampling Process

The innovative resampling technique developed in this study effectively reduced each dataset’s size to approximately 1,500 points, while still preserving the critical resonance structures integral to nuclear reactions. This level of compression was achieved without compromising the data’s fidelity, which is vital for accurate simulations.

Error Metrics for Benchmarking

To ensure the integrity of the resampled datasets, various error metrics were computed. These included:

• Mean Squared Error (MSE)
• Mean Absolute Error (MAE)
• Root Mean Squared Error (RMSE)
• Coefficient of Determination ((R^{2}))

These metrics quantified how closely the resampled datasets matched the original datasets, offering insights into the efficacy of the compression technique.

Comparison Against Supervised Regressors

Further evaluation involved benchmarking the resampled cross sections against predictions made using two supervised regression models: K-Nearest Neighbors (KNN) and Gaussian Process Regression (GPR). The results were displayed in log-log plots to effectively communicate findings across the extensive energy domains relevant to reactor physics.

Performance Metrics Analysis

The quantitative evaluation presented in Table 3 illustrated the competency of the developed method across all tested temperatures. Notably, the Developed Method consistently attained (R^{2}) values near or above 0.99, showcasing its ability to reproduce sharp resonance peaks and threshold transitions accurately.

Observations on KNN and GPR

While the KNN interpolant offered reasonable accuracy, it exhibited local errors when the sampling density was insufficient. GPR performed well, especially with short length-scale kernels, but required meticulous hyperparameter tuning to accurately predict extreme resonance structures.

Temperature-Specific Observations

The robustness of the developed method was evident across different temperatures, particularly in how it preserved critical spectral features. For instance, as temperature increased, the relative motion between neutrons and nuclei led to Doppler broadening of the resonance structures.

Data Preservation at High Temperatures

Predictions at high temperatures of (1200\,\text{K}) and (2500\,\text{K}) indicated that, although resonance structures were somewhat smeared, the resampling still maintained a high density of sampling points in resonance-dominated energy ranges. Both absolute and relative error metrics remained low, affirming the approach’s efficacy.

Comparing Classical Approaches with the Developed Method

The developed method employed a region-specific weighting, effectively mitigating localized interpolation errors typically associated with KNN. Conversely, GPR’s reliance on kernel methods managed to capture minute details but could become computationally prohibitive when handling large datasets.

Integrating with OpenMC

A particularly advantageous aspect of the developed approach lies in its direct modification of HDF5 files, facilitating real-time updates of cross-section data in sensitive analyses without convoluted file conversions.

Error Analysis: Absolute and Relative Metrics

Extended error analyses highlighted the adaptive sampling approach’s strength in preserving critical resonance behaviors across thermal, epithermal, and resonance domains. The adaptive grid maintained dense sampling where the change in cross-section was significant, while thinning in smoother energy regions conserved essential data without excess volume.

Error Metrics Overview

• Thermal and Epithermal Range ((E \lesssim 0.3) eV): Mean absolute error remained under 5 barns.
• Resolved Resonance Region (0.3 eV–2.25 keV): Relative errors fluctuated between 0.6% and 2%, showcasing a high fidelity to resonance features.
• Unresolved Resonance Band (2.25 keV–25 keV): Both temperatures exhibited minimal errors, maintaining precision.

Probabilistic Uncertainty Envelope

A non-parametric bootstrap analysis was performed to assess the sensitivity of the adaptive grid. The 95% confidence envelope yielded bands that remained mostly below 1 barn across various domains, further supporting the method’s ability to mitigate stochastic sampling deviations.

Future Work: Benchmarking Against NJOY’s RECONR

The present study sets the stage for an upcoming evaluation against NJOY’s RECONR module, which will explore the effectiveness of this approach across multiple nuclides and temperatures. This future analysis promises to reinforce the developed method’s advantages in terms of speed and fidelity in processing nuclear data.

By offering a streamlined, effective solution for handling U-235 fission cross sections, the adaptive resampling strategy presents a promising avenue for enhancing nuclear simulation workflows, allowing for both accuracy and efficiency in critical applications.