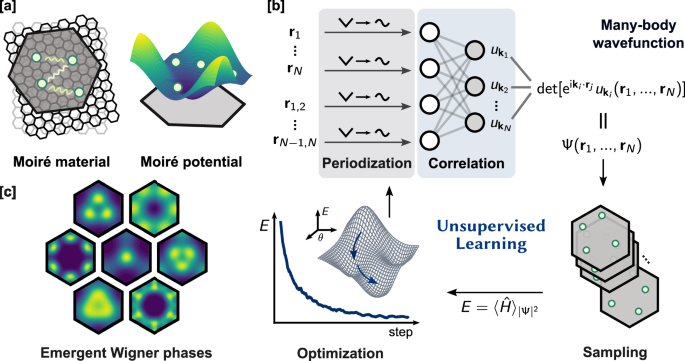
Deep Learning Architecture for Quantum Phases in Moiré Materials
The intersection of deep learning and quantum physics paves the way for groundbreaking explorations in complex materials known as moiré materials. These structures emerge when two layers of van der Waals materials overlap with mismatched lattice constants or twisted angles, leading to a rich variety of quantum phases. To unravel the intricate quantum states within these materials, researchers have turned to neural networks to represent many-body wavefunctions, fundamentally altering our approach to understanding condensed matter systems.
The Neural Network Wavefunction
At the heart of this exploration is the neural network wavefunction, denoted as Ψ_net. This is mathematically represented in a striking manner:
$$
\begin{array}{c}
\Psi{{{{\rm{net}}}}}=\det [{e}^{i{{{{\bf{k}}}}}{i}\cdot {{{{\bf{r}}}}}{j}}{u}{{{{{\bf{k}}}}}{i}}({{{{\bf{r}}}}}{1},…,{{{{\bf{r}}}}}_{N})]\,.
\end{array}
$$
This equation captures the complex interactions among particles constrained by the moiré potential and their Coulomb interactions. The neural network takes into account all particle features—represented as r_i—transforming them into periodic inputs for a permutation-equivalent architecture. The resulting function incorporates generalized Bloch functions alongside a Slater determinant, forming a periodic and antisymmetric many-body wavefunction. By embedding millions of parameters into this network, it effectively embodies the diverse symmetries of quantum states.
Variational Monte Carlo Optimization
Utilizing the neural network wavefunction alongside the Hamiltonian of the material, researchers can harness the variational Monte Carlo (VMC) method to optimize the parameters of the neural network. VMC capitalizes on a fundamental principle of quantum mechanics: the ground state must possess the lowest energy among all possible solutions, refining the training process into an unsupervised learning journey. This self-correcting mechanism enhances the reliability of the deep learning architecture as it converges toward accurately describing quantum states.
Understanding Moiré Superlattices
Moiré superlattices are the result of overlapping van der Waals materials, where their unique lattice interactions create a significantly larger effective lattice constant that can house thousands of atoms within a single unit cell. Given the inherent complexity, traditional methods using full ab initio Hamiltonians proved impractical for analyzing these materials. Instead, researchers focus on low-energy effective Hamiltonians, which simplify the problem while retaining critical features like Coulomb interactions:
$$
\begin{array}{c}
\hat{H}=\sum\limits{i}\left[-\frac{{\Delta }{i}}{2{m}^{* }}+{V}{M}({{{{\bf{r}}}}}{i})\right]+\frac{1}{2}\sum\limits{i\ne j}\frac{1}{\epsilon | {{{{\bf{r}}}}}{i}-{{{{\bf{r}}}}}{j}| }\,,
\
{V}{M}({{{\bf{r}}}})=-2V{\sum }{i=1}^{3}\cos ({{{{\bf{b}}}}}{i}\cdot {{{\bf{r}}}}+\phi )\,.
\end{array}
$$
This model captures doping holes in transition metal dichalcogenides (TMDs) near the Fermi surface, exhibiting simplified behavior while still being rich in correlations, which are crucial for studying emergent states like Wigner crystals.
Emergent Quantum Phases: Wigner Crystals
The concept of Wigner crystals dates back to 1934, when Eugene Wigner theorized that electrons could spontaneously organize into structured patterns at lower densities. This idea has gained momentum in the context of moiré materials, with researchers using deep learning to replicate experimentally observed Wigner phases. Initial findings demonstrate a Mott insulating phase at half filling, displaying the strong correlation characteristics inherent to these systems.
Moreover, various Wigner crystal phases have been identified at fractional fillings with symmetry-breaking behaviors that correspond to recent experimental measurements. Through advanced deep learning techniques, researchers have validated the neural network’s capacity to capture complex phenomena that arise from correlated electron systems.
Wigner Molecular Crystals and More
As research progressed, attention shifted to the formation of Wigner molecular crystals, where multiple particles aggregate at a minimum in the moiré potential. This phenomenon leads to intriguing molecular formations observable through states like WSe2/WS2 heterobilayers. Here, the ability to predict various filling patterns and their corresponding ground states becomes crucial. For instance, at filling levels ν = 2, the Sz = 0 state emerges as the lowest energy configuration.
At higher filling regimes, complex interactions, such as Coulomb repulsion and Pauli exclusion, shape the resulting ground state configurations. Novel states such as the Wigner covalent crystal emerge when interactions among particles facilitate bonding-like behavior, mimicking chemical covalence.
Expanding the Frontier: Predicting New Phases
Having established a robust methodology capable of reproducing known quantum phases, researchers are now venturing into previously unexplored territory. For example, examining different structural configurations like the 3R configuration of WS2 unveils remarkable symmetry-breaking phenomena, particularly in the behavior of filling patterns characterized by C6 and C3 symmetry.
Through careful manipulation of interaction ratios, further insights into potential phase transitions can be acquired. The burgeoning research in deep learning approaches not only solidifies existing theoretical frameworks but also unlocks pathways for predicting novel quantum states—propelling forward the study of moiré materials and their exotic properties.
This innovative application of neural networks meshes sophisticated theoretical approaches with cutting-edge technology, offering a fresh lens through which to view and understand the quantum phenomena that govern the behavior of these fascinating materials. As the field progresses, the collaboration between machine learning techniques and condensed matter physics promises to reveal even more surprises, enriching our understanding of the quantum world.