Understanding Coherent Optical Seeds in Incoherent Modulation Instability Dynamics
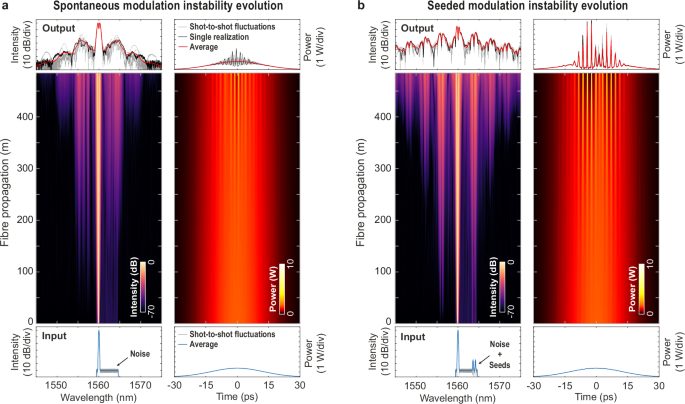
The fascinating interplay of coherence and noise in nonlinear optical fibers offers intriguing possibilities for controlling light propagation, essential for various applications in photonics. Our study elucidates this principle, as illustrated in Figure 1, which presents a streamlined and impactful method for utilizing coherent optical seeds to mitigate and tune the chaotic nature of incoherent dynamical evolution stemming from concurrent noisy processes.
A Closer Look at Incoherent Modulation Instability Dynamics
Spontaneous Modulation Instability Dynamics
The process of spontaneous modulation instability (MI), depicted in Figure 1a, arises when a coherent optical pulse interacts with an incoherent noise field in a nonlinear fiber. This phenomenon triggers broadband noise amplification, leading to complex cascaded four-wave mixing processes. As a result, the output spectrum broadens significantly, characterized by substantial shot-to-shot fluctuations rooted in varying input noise conditions.
In the temporal aspect, highly localized pulse structures emerge, which, when averaged over multiple realizations, often go unnoticed (as shown with the averaged red lines). The complications in identifying distinct signal patterns underline the randomness introduced by the incoherent noise.
Seeded Modulation Instability Dynamics
By introducing weak yet coherent optical seeds that co-propagate with the noisy input pulse, as illustrated in Figure 1b, we navigate this complexity with greater efficiency. This seeded MI scenario allows for significant modulation of the propagation dynamics, facilitating a relative control over the spectral broadening processes foreseeable in the initial noise-driven context. Although the output waveform remains largely incoherent—reflecting shot-to-shot fluctuations detailed in the corresponding averages—this approach fosters an observable structuring in the output profiles.
Such modifications prompt our investigation into utilizing artificial neural networks (ANNs) to predict propulsion characteristics derived from extensive datasets generated from numerical simulations and experiments.
Harnessing Artificial Neural Networks for Prediction and Inference
ANN Architecture
Our ANN framework (illustrated in Figure 2) operates through a dual-propagation approach, encompassing both forward and backward dynamics. The forward model predicts incoherent dynamics based on initial seed conditions, while the backward model infers these input conditions from the corresponding output features. Using a standardized 5-layer neural network architecture ensures reproducibility, treating both input and output layers to handle varying seed parameters or spectral features.
Training Methodology
The backbone of our approach lies in thorough numerical simulations—specifically, Monte Carlo analyses of optical pulse propagation. Each simulation considers diverse broadband white noise scenarios and amplified spontaneous emission (ASE) noise to comprehensively assess coherence dynamics. This extensive numerical dataset, comprising over 50 million spectra from approximately 100,000 seed configurations, provides the necessary material for training our ANNs.
By evaluating the ANN’s capacity to predict average spectra ( S(\lambda) ) and correlation properties from the noisy realizations, we unveil the promising potential of deep learning in deciphering complex nonlinear optical systems.
Performance Benchmarking of the ANN
Numerical Predictions and Inferences
Upon testing our ANN on various configurations, the outcomes indicate robust predictive accuracy. The ANN distinguishes itself in forecasting average output spectra from dual-seed configurations with a mere 1.0% root mean square error (RMSE) against ground truth derived from numerical simulations. Moreover, it infers seed parameters such as wavelengths and relative phases with an impressive RMSE averaging below 2.4%. This accuracy is particularly striking given the inherent challenges posed by weak signal amplification and complex noise dynamics.
Figures 3a and 3b exhibit the ANN’s adeptness in retrieving insights, demonstrating that even in noise-saturated environments, the designed architecture can unearth valuable information regarding spectral fluctuation and correlation, crucial for applications spanning incoherent imaging and quantum signal processing.
Transition to Experimental Validation
Building upon qualitative comparisons established through simulations, we shifted focus toward experimental validation of the ANN framework. Our experimental setup, shown in Figure 4, allows real-time spectral characterization, integrating sophisticated technological elements such as dispersive Fourier transform (DFT) for temporal trace analysis. This stage solidifies the link between theoretical predictions and practical implementation.
From this complex experimental environment, we gathered vast datasets to examine the influences of coherent optical seeding on MI dynamics. Results affirm the ANN’s potential in this practical realm, yielding RMSE below 5.0% for wavelength inference and down to 7.3% for phase retrieval, showcasing the model’s robustness even amid real-world challenges.
Exploring the Capacity to Mitigate Nonlinear Dynamics Through ANNs
As we delve deeper into the ANN’s learning and adaptation capabilities, the framework continuously proves its utility in tracking and predicting the statistical fluctuations inherent in incoherent modulation instability. Using numerical datasets, we train the ANN to generate correlation maps ( \rho_n(\lambda, \lambda) ), yielding insight into the spectral properties and merging stability with chaotic nonlinear mixing processes.
Predictive Capacity in Experimental Conditions
In practical scenarios, however, the intricacies of nonlinear optical systems introduce unpredictability due to inherent variabilities such as noise dynamics and amplifier instability. This presents an opportunity for ANN methodologies to outperform traditional analytical tools. Figures 6 and 7 illustrate our advances in predicting spectral correlation maps from both numerical simulations and experimental data. The ANN demonstrates strong predictive performance, achieving RMSE values as low as 3.9% to 8.1% across various seeding configurations, thereby confirming its capability to discern essential characteristics from complex input parameters.
By leveraging both the spectral intensity of output signals and tailored initial conditions for training, the ANN can effectively navigate intricate nonlinear light propagation scenarios. Its ability to forecast spectral correlation signatures amid challenging experimental settings highlights its practical applicability in modern photonics research.
Through these structured investigations, we spotlight the critical fusion of deep learning techniques with traditional optical research, promising a future where complex nonlinear dynamics can be efficiently analyzed and controlled. This sets a precedent for exploring new methodologies and technologies that harness the inherent disorder of optical systems, pushing the boundaries of what is possible within the field.