Exploring Hyperparameter Tuning in Machine Learning: A Comparative Analysis of MLP and CNN Techniques
In the expanding landscape of machine learning (ML), the concept of hyperparameter tuning is a critical element that can profoundly affect the performance of different models. In particular, this article delves into the comparison of hyperparameter tuning approaches for Multi-Layer Perceptrons (MLPs) and Convolutional Neural Networks (CNNs), highlighting the complexities involved and showcasing experimental methodologies and results.
Hyperparameter Space Exploration
The hyperparameter values critical for training machine learning models are summarized in Tables 2 and 3, detailing key hyperparameters for MLP and CNN architectures, respectively. In examining the search space, MLP hyperparameters yielded 23,040 combinations, while the CNN’s hyperparameter configurations soared to an extraordinary 637,009,920.
The significant disparity in these numbers can be attributed to CNNs’ unique architectural features. While MLPs mainly optimize for layer widths and depths, represented mathematically as ( \mathscr{O}(n^L) ) (where ( n ) is the number of neurons and ( L ) is layer depth), CNNs add additional layers of complexity. This complexity introduces parameters like kernel sizes, strides, pooling operations, feature maps, and specialized connectivity patterns (such as residual connections), leading to a multiplicative increase in possible configurations formulated in ( \mathscr{O}(n^L \times k^L) ).
Methodology Considerations
As outlined in Table 4, the experimental parameters used in this study establish the foundation for effective model training. While ideally, an exhaustive search through all combinations would yield an optimal model, temporal and memory limitations necessitated a strategic approach—a fixed number of 200 generations for the Genetic Algorithm (GA). Both the Random Search (RS) and GA methods were limited to these 200 iterations, assuming this would provide a comprehensive exploration of the hyperparameter space.
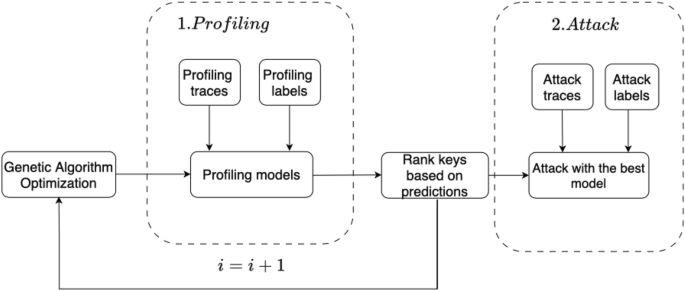
The foundational structure of the algorithm unfolds in two key phases. As depicted in Figure 2, the initial stage involves random selection from the hyperparameter combinations of MLP or CNN structures. Subsequent steps involve machine learning training, where multiple chromosomes generate profiling models through selection, crossover, and mutation. The top-performing models advance to create the next generation of potential solutions, culminating after 200 iterations in the selection of an optimal model, which is further retrained for operational use.
Experimental Context and Datasets
Utilizing both the ASCADf and ASCADr datasets for this experiment opened avenues for diverse testing scenarios. The following discussion elucidates the findings derived from these datasets, beginning with the fixed key scenario of the ASCADf dataset.
ASCAD Fixed Key: Key Predictions and Model Performance
In this analysis, the validation key rank served as the objective function, with models trained over 10 and 50 epochs. Figure 3 highlights the MLP performance under the Identity (ID) leakage model, where GA efficiently predicted the secret key requiring just 121 traces after 10 epochs, compared to 268 for the RS method. For 50 epochs, GA maintained its advantage, needing 190 traces versus RS’s much heavier 2072 traces.
Transitioning to the Hamming Weight (HW) leakage model, Figure 4 illustrates a similar result: GA outperformed RS consistently, predicting the secret key with significantly fewer traces—714 for GA compared to RS’s 986 after 10 epochs, and 1012 to RS’s 1579 in the 50-epoch training phase.
Assessing CNN Performance Under Fixed Key Conditions
Extending our evaluation to CNNs presented an intriguing contrast. Under the ID leakage model depicted in Figure 5, the GA required 322 traces compared to RS’s 379 in a ten-epoch training arrangement. A noticeable disparity emerges at the 50-epoch training, where GA still outperformed RS.
The HW leakage model further accentuated the efficacy of GA, obtaining the best performance metrics once again for both the 10 and 50-epoch configurations, affirming the genetic algorithm’s superior capacity to navigate expansive search spaces effectively.
ASCAD Variable Key: Complexity in Key Recovery
Switching focus to the ASCAD variable key dataset unveils differing challenges. The GA’s performance was notably less effective here when comparing varying key scenarios illustrated in Figures 7 and 8. In the ID leakage model, for instance, while GA performed adequately, RS yielded better results, requiring fewer traces for successful key recovery.
Figure 9 illustrates the performance of CNN under variable key scenarios. Interestingly, the GA model only successfully predicted the secret key in the fifty-epoch training, showcasing its potential limitations when faced with more complex datasets.
Robustness and Comparative Performance
An extensive robustness analysis revealed significant findings when conducting multiple trials using the variable key dataset. Fisher’s exact test indicated a meaningful statistical difference between GA and RS, with the GA achieving a 10% success rate. This assertion underscores the reliability of GA’s performance, solidifying its validity as a robust hyperparameter tuning strategy.
When juxtaposing GA against other hyperparameter optimization methodologies, the findings substantiate GA’s inherent advantages, such as adaptability to varying scenarios and flexible search capabilities. This is particularly valuable in practical applications where environment conditions may shift unpredictably.
Future Directions
The implications of this study pave the way for subsequent investigations into alternative evolutionary algorithms like Particle Swarm Optimization (PSO) and Differential Evolution (DE). Although GA demonstrated commendable performance, exploring these alternatives could potentially enhance hyperparameter tuning across diverse datasets and complexities.
With the continual evolution of machine learning techniques, our understanding of hyperparameter tuning will only deepen, driven by ongoing research and experimental innovations. The search for optimal models is far from over, and techniques like GA will play an essential role in addressing the challenges posed by increasingly complex datasets.