Experimental Data Set
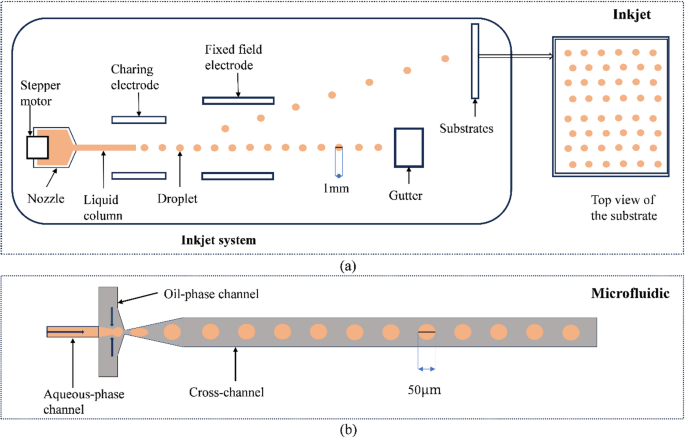
In this research, we conducted experiments using two distinct droplet image datasets: one derived from a millimeter-scale inkjet device and the other from a microfluidic device. The dataset for the inkjet device stems from previous work by Siemenn et al. (2022), presenting a rich foundation for our analysis and validation.
Inkjet Device Parameters and Dataset
The inkjet device’s performance is influenced by three critical control parameters: fluid pressure, piezoelectric drive frequency, and nozzle translation speed. Each of these variables plays a significant role in shaping the droplets that are deposited on the substrate. Our experimental dataset contains 140 droplet images that exemplify a wide array of scenarios—ranging from cases where no droplets are produced, to instances of unusually large droplets, to satellite droplets, culminating in the ideal droplet formations. This extensive compilation highlights the diverse outcomes that can result from varying the control parameters.
Microfluidic Device Dynamics
Conversely, the microfluidic device operates using two primary control parameters: water pressure and oil pressure. The dataset for this device also comprises 140 droplet images. These images depict droplets formed during contraction without making contact with the contraction wall, droplets that do come into contact under varying droplet generation mechanisms, and instances of no droplet formation at all. This comprehensive dataset is essential for exploring the nuances of droplet formation within microfluidic systems as detailed by Nguyen et al. (2022) and Liu et al. (2021).
Demonstration of Gaussian Process Model Fitting
In Bayesian Optimization (BO), the Gaussian Process (GP) serves as a useful tool to construct a proxy model of the objective function. This model not only helps in estimating the predictive mean and variance but is integral in the formulation of the Expected Improvement (EI) function. The EI function is essential as it governs the selection of the next sampling point, thereby directing the optimization towards the global optimum.
To evaluate the effectiveness of the GP in fitting the objective function, we began with an initial sample and compared the predicted objective function values derived from the GP model against the true values. This comparison utilized metrics like the Mean Square Error (MSE) and the coefficient of determination (R²). A lower MSE alongside a higher R² indicates a well-fitted model. Validating this using various plots illustrated our model’s accuracy, confirming its robustness in predicting objective outcomes.
Bayesian Optimization Results
The flowchart illustrating our BO optimization process unveils a dynamic interaction between droplet image processing and BO. Initially, droplet images undergo watershed segmentation, a critical step for achieving clear differentiation between the droplets and their backgrounds. Subsequently, these segmented droplets are analyzed through quantifying metrics relating to geometric properties, yield, and size uniformity, creating input parameters for the GP model.
Each optimization stage produces two minimum objective function values along with their predicted parameters, and after performing 50 rounds of iterative optimization, we amassed 100 prediction sets. Analyzing the implications of this data revealed that the objective function values consistently continued to decline, reflecting the success of our optimization efforts.
Comparison Testing of Optimization Methods
To validate the predictions generated by the GP-BO methodology, we compared outputs from this approach against the previous iterations of the BO in Loop method documented in the literature. The objective function utilized was {l′(x)}, initially aimed at optimizing the device control parameters. Notably, to mitigate the influence of irregular satellite droplets, we incorporated an improved objective function {l(x)} that factors in dimensional uniformity loss.
Observing the parallel coordinate plots generated from both optimization methods showcased a striking similarity in outputs, reinforcing the reliability of our analysis. The GP-BO method highlighted better parameter performance, particularly in achieving ideal droplet formation under lower piezoelectric drive frequencies and faster nozzle speeds.
Moreover, the box plots illustrating the predicted parameter values revealed that the GP-BO method provided tighter distributions around the median, indicating stable and consistent predictions compared to the earlier optimization method. This implies that our new method not only optimizes droplet formation but also enhances the predictability of these operations.
Summary of Findings
In summarization, our research showcases the potential and efficacy of the GP-BO optimization method in producing more accurate results compared to the traditional BO in Loop method. The extensive dataset derived from both the inkjet and microfluidic devices serves as a robust framework for evaluating droplet formation dynamics. Each facet of the experimental setup—from control parameters to the analysis of the optimization process—paints a comprehensive picture of advancements and insights in the realm of droplet generation technology. This thorough exploration into the experimental parameters and results emphasizes the application of machine learning and computer vision to further innovation in fluid dynamics and material science.