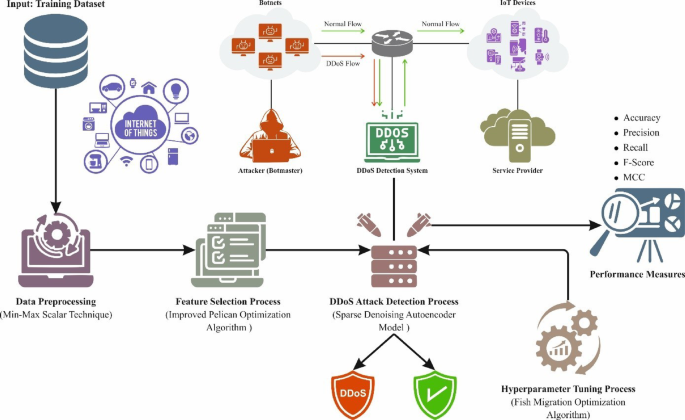
An Advanced Approach to DDoS Attack Detection in IoT Networks: The FPODL-DDoSAD Method

In the rapidly evolving landscape of the Internet of Things (IoT), security has emerged as a paramount concern due to the exponential increase in devices connected to the internet. This article introduces a novel and efficient method known as FPODL-DDoSAD, aimed specifically at identifying Distributed Denial-of-Service (DDoS) attacks within IoT networks. The technique encompasses several integral processes, including data normalization, an Intelligent Pelican Optimizer Algorithm (IPOA)-based feature selection (FS), Sparse Denoising Autoencoder (SDAE)-based cyberattack detection, and Fish Migration Optimization (FMO)-based parameter selection.

Data Normalization

The initial step in the FPODL-DDoSAD methodology involves normalizing data to ensure that it’s in a standard format. Min-max normalization, a technique that scales data to a specific range, typically between [0,1], plays a crucial role here. This method is favored for its simplicity and efficiency. By keeping all features within a consistent range, it ensures that no single feature disproportionately affects the model, which is particularly vital for machine learning (ML) algorithms sensitive to changes in input scale, such as those employed in gradient descent methods.

Unlike z-score normalization, which can introduce negative values that some algorithms may be ill-equipped to handle, min-max normalization maintains positivity, making it exceptionally suited for various applications that demand non-negative inputs. Its computational efficiency also makes it ideal for large datasets and real-time applications, balancing effectiveness with ease of implementation.

The min-max normalization process can be mathematically represented as:

[
\text{x}^{\prime} = \frac{{\left( {x – x{\text{min}} } \right)}}{{\left( {x{\text{max}} – x_{\text{min}} } \right)}}
]

where (x) is the original value, (x{\text{min}}) and (x{\text{max}}) denote the minimum and maximum feature rates, respectively.

This normalization technique ensures that features with various numerical ranges do not skew the model’s training performance, ultimately promoting faster convergence and improved results.

Feature Selection Process

Following data normalization, the FPODL-DDoSAD framework employs the Intelligent Pelican Optimizer Algorithm (IPOA) for feature selection. IPOA mimics the hunting strategies of pelicans, allowing for efficient exploration and exploitation of the search space to identify an optimal subset of features.

The algorithm operates on the principles of nature-inspired optimization, balancing exploration (scouting for better solutions) with exploitation (refining known solutions). In comparison with traditional techniques such as Genetic Algorithms (GA) and Particle Swarm Optimization (PSO), IPOA offers enhanced convergence speeds and effectively circumvents local optima.

By employing IPOA for feature pruning, the FPODL-DDoSAD framework optimizes the feature subset, thereby boosting accuracy while minimizing redundancy and ensuring the robustness of ML techniques.

Mathematical Representation

IPOA constructs potential members using the equation:

[
x_{i,j} = l_j + \text{rand}(u_j – l_j), \quad i = 1,2,3,\ldots, N, \quad j = 1,2,3,\ldots, m
]

Here, (x_{i,j}) refers to the position in the (i^{th}) dimension, while (rand) generates a random number within the range [0, 1].

As the pelican hunts, it undergoes exploration and exploitation phases, which iteratively adjust feature values in pursuit of the optimal configuration.

Cyberattack Detection Using the SDAE Classifier

The next phase of the FPODL-DDoSAD methodology encompasses cyberattack detection through the implementation of the Sparse Denoising Autoencoder (SDAE) model. This method is particularly adept at handling noisy and incomplete data, making it especially suitable for distinguishing between genuine network activity and malicious DDoS attacks.

The SDAE model excels at learning robust representations by denoising inputs and extracting critical patterns to detect subtle and complex attack behaviors. Unlike traditional classifiers, SDAE employs deep learning techniques that can model non-linear relationships within data, significantly enhancing detection accuracy.

Structure and Functions of SDAE

The SDAE consists of two primary components: encoding and decoding. The encoder maps high-dimensional input data into a lower-dimensional representation, facilitating dimensionality reduction. Conversely, the decoder reconstructs the input from this compact representation, effectively reproducing the original data.

Mathematically, the process can be framed as follows:

[
h = f(W_1 x + \lambda_1)
]

where (h) represents the features extracted through the encoder, (W_1) is the encoder weight, and (\lambda_1) is the bias term.

The learning objective of SDAE is to minimize the reconstruction error, thus capturing essential features from the input dataset and enhancing the model’s performance in distinguishing legitimate traffic from attack traffic.

Loss Function

An important aspect of SDAE’s effectiveness is its loss function, which can be represented mathematically:

[
L{AE} = \frac{1}{n} \sum{i=1}^{n} (x_i – y_i)^2
]

where (x_i) and (y_i) represent the input and the output of the autoencoder, respectively.

The implementation of noise coding and sparsity constraints further boosts the performance of the SDAE model by improving feature generalization while reducing overfitting.

Parameter Selection

Finally, optimal parameter selection for the SDAE model is achieved through the Fish Migration Optimization (FMO) method. This approach’s strength lies in its ability to dynamically adjust parameters for high adaptability, ensuring the model’s performance remains robust even in complex optimization landscapes.

FMO mimics the migration behaviors of fish, emphasizing a balance between exploration and optimization, which mirrors the challenges encountered in high-dimensional parameter spaces. Unlike conventional optimization techniques like Grid Search and Random Search, FMO provides swift convergence while minimizing computational overhead.

Phases of the FMO Method

The stages of the FMO process draw on the life cycle of the grayling fish, divided into five distinct phases, each associated with varying reproductive abilities. These phases influence the optimization strategy within the FMO framework, allowing for simulations of swimming and migration dynamics in search of optimal solutions.

Mathematical representations within the FMO model facilitate energy handling and movement dynamics, refined to expedite convergence:

[
E_{r,d} = \text{rand} \cdot E
]

The effective correlation between the distance moved and energy consumption is described in further detail:

[
dis{offset,d} = \frac{E{r,d} \cdot U{s,d}}{a + b \cdot (U{s,d})^{x}}
]

These formulations help maintain optimal parameters throughout the iterative process, enhancing the overall effectiveness of the FPODL-DDoSAD methodology.

The FPODL-DDoSAD framework is thus positioned as a comprehensive approach to DDoS attack detection in IoT networks, comprising innovative techniques for data normalization, feature selection, cyberattack identification, and parameter optimization, each contributing to its ability to evolve with the dynamic complexities of network security challenges.