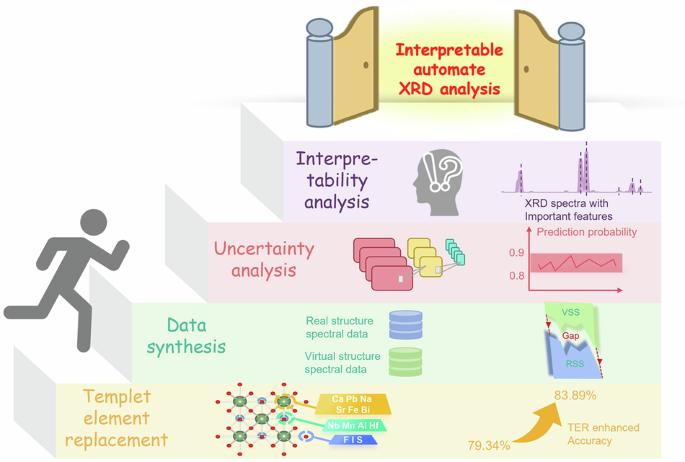
Framework for XRD Prediction and Its Analysis

Understanding the Background: Virtual and Real Structure Spectra

When discussing X-ray diffraction (XRD) analysis, one must differentiate between virtual structure spectra (VSS) and real structure spectra (RSS). VSS are synthesized using structural templates that encompass a broad range of hypothetical and often unstable structures. This diversity can facilitate learning general structure-spectrum relationships, yet it introduces discrepancies from actual experimental spectra simply because these virtual structures may not align with the intricacies of real materials.

In contrast, RSS are derived from experimentally validated, stable structures available in the Inorganic Crystal Structure Database (ICSD). Given that these structures are physically confirmed, the corresponding spectra are likely to replicate real-world experimental conditions more accurately than their virtual counterparts. This understanding positions RSS as the “ground truth” necessary for evaluating prediction models.

To address the physical discrepancies between VSS and RSS, this study employed a data synthesis technique that aligns datasets according to their classification labels. This strategy aims to assess whether the mappings learned from VSS can enhance the model’s predictive capabilities regarding real structure XRD spectra, ultimately improving phase identification accuracy in experimental contexts.

The Role of B-VGGNet: Architecture and Innovation

The backbone of this method is the B-VGGNet, an iteration of the VGGNet originally designed for computer vision applications. Adapting this model for XRD data involves classifying and predicting crystalline spatial clusters and structures. A Bayesian layer was integrated into the penultimate stage of the network, allowing for model uncertainty to be evaluated.

The Bayesian layer employs three methodologies: Monte Carlo Dropout (MCD), Variational Inference (VI), and Laplace Approximation (LA). Each method works to ascertain the contribution of different features in the classification, tapping into their physical significance. By doing so, the model enables insightful interpretations of classification results, marrying the robust capabilities of deep learning with Bayesian statistical methods.

Dataset Construction: Exploring Perovskite Diversity

A crucial component of this research revolves around constructing a dataset that thoroughly investigates the structural diversity inherent in perovskite compounds. Perovskites, characterized by an ABX₃ stoichiometry, showcase extraordinary structural flexibility. The central B site is enclosed within BX₆ octahedra, allowing for numerous arrangements and distortions.

This research began with a detailed analysis of 93 space groups conducive to ABX₃ frameworks within the Materials Project (MP) database. In parallel, 53 perovskite chemical formulas were identified from the ICSD, establishing real structure templates. Given the inherent flexibility of the perovskite lattice, this systematic approach allows for the generation of hypothetical compounds by substituting chemically compatible elements into existing templates.

The pathway to successful element substitution is grounded in maintaining charge neutrality, as illustrated by the equation:

[
\text{valence}(A) + \text{valence}(B) + 3 \times \text{valence}(X) = 0
]

Automated scripts were crafted to analyze CIF files of template structures, facilitating identification and substitution of A- and B-site elements while adhering to a pre-defined list of compatible elements. This rigorous process resulted in a robust dataset consisting of 4,929 chemically valid perovskite candidates.

Data Simulation and Alignment: Bridging the Gap

To simulate realistic XRD spectra, the research incorporated the Python Materials Genomics (pymatgen) library. This simulation process included element-specific Debye–Waller factors to enhance accuracy by accounting for thermal vibrations. In instances where reliable experimental data were unavailable, comparable values from similar species were adopted to ensure consistency.

The challenge lies in the gap between VSS and RSS, which can hinder the performance of deep learning models. To bridge this divide, the study introduced a series of augmentation processes, including the simulation of unintended phases or contaminants, which are frequently encountered in experimental contexts. By embedding random impurity peaks into the VSS, the datasets became more representative of practical scenarios, enhancing the robustness of the predictive model.

Furthermore, the methodology varied peak intensities to reflect preferred crystallographic orientations within samples, adjusting intensities by up to ±50%. Other factors such as grain size variations and lattice strain were also simulated to account for common discrepancies seen in real XRD analysis. This comprehensive strategy ultimately elevated the realism of the virtual datasets.

B-VGG Model Construction: Tailoring the Architecture

Transitioning into model creation, the study adapted the VGGNet architecture specifically for XRD data. This transformation incorporated 1D convolutional layers activated by ReLU functions, which effectively captured the intricacies of XRD patterns.

To mitigate overfitting, the model’s architecture was meticulously optimized, ensuring a balance between detailed feature extraction and generalization capabilities. Max-pooling layers were integrated to distill key features necessary for effective classification.

A noteworthy advancement of the B-VGGNet was the incorporation of Bayesian Neural Networks (BNNs). These networks quantify the uncertainty embedded in predictions, crucial given the variability inherent in experimental data. Employing a probabilistic framework allowed for weight distributions that better captured both epistemic and aleatory uncertainties.

Uncertainty Analysis: Evaluating Prediction Reliability

The implementation of Monte Carlo dropout (MCD) emerged as an effective technique for estimating uncertainty within the deep neural network. By training the model with dropout layers active during inference, multiple forward passes generated a range of predictions that approximate samples from the model’s posterior output.

Conversely, the Laplace Approximation (LA) method is utilized to estimate posterior distributions in BNNs. The process involves calculating the Hessian matrix around the maximum a posteriori (MAP) estimates to derive covariance for Gaussian approximations, further enhancing the model’s reliability.

Variational Inference (VI) also played a pivotal role, facilitating the approximation of posterior distributions for model weights. By minimizing the Kullback-Leibler divergence between a selected variational distribution and the true posterior, the study resulted in multiple B-VGGNet models, each characterized by its unique approximated distribution.

SHAP Value Computation: Enhancing Model Interpretability

To elucidate the contributions of individual diffraction angles to the predictions made by the B-VGGNet model, the SHAP (SHapley Additive exPlanations) method was deployed. Grounded in cooperative game theory, SHAP provides a structured approach to interpret machine learning outputs by computing the Shapley value for input features.

For each feature corresponding to XRD patterns, SHAP values highlight how their presence shifts model predictions, offering critical insights into the model’s decision-making process. This interpretability feature is not just theoretical; it operationalizes a deeper understanding of the model’s behaviors across different space groups, driving improvement in future iterations of the model.

By employing this comprehensive framework for XRD prediction, the study unites advanced computational methodologies with rigorous statistical analysis, setting a foundational precedent for further explorations into the intricate relationship between material structures and their spectroscopic signatures.