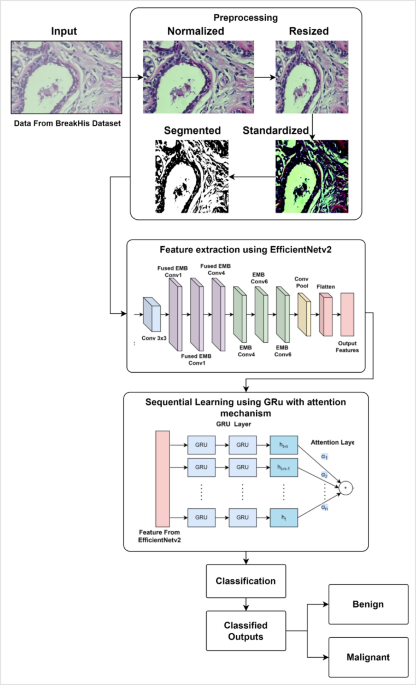
Preprocessing Images for Deep Learning in Histopathology

The preliminary step in any deep learning model, especially in the context of histopathology image analysis, is the preprocessing of input images. This essential phase serves to convert raw image data into a format that aligns with the requirements of the deep learning architectures being used.

Image Representation

The original input image, denoted as (\:I), can be viewed as a matrix of size (\:(H \times W \times C)), where:

• (\:H) signifies the height,
• (\:W) denotes the width, and
• (\:C) stands for the number of channels (RGB, for instance).

In order to maintain uniformity within the model, the images are reformatted into a standardized size of (\:(H_s \times W_s \times C)), where the transformation can be mathematically represented as:

[
{I}{1}=T\left(I,{H}{s},{W}_{s}\right)
]

Here, (\:T) is a transformation function designed to adjust the original dimensions of the image to the preset target dimensions.

Resizing and Normalizing

In the preprocessing phase, histopathology images are resized to a fixed dimension of (224 \times 224 \times 3) pixels. This choice aligns with the input size of EfficientNetV2, which is carefully selected to retain crucial cellular and structural information while optimizing computational requirements.

After resizing, the next step involves normalization. Normalization is vital as it scales pixel intensity values from the range [0, 255] to a standardized [0, 1]. This procedure can be expressed mathematically as:

[
{I}_{2}=\frac{I(x,y)}{255}
]

This transformation involves dividing each pixel intensity ({p}_{ij}) at coordinates ((i,j)) by the maximum intensity of 255, which enhances numerical stability during gradient computation and assists in rapid convergence during training.

Standardization

Following normalization, the next step is standardization, utilizing the mean ((\mu=0.485)) and standard deviation ((\sigma=0.229)) values from the ImageNet dataset. This adaptation is paramount as EfficientNetV2 is pretrained on ImageNet, thereby facilitating better feature extraction performance.

[
{I}{3}=\frac{{I}{2}-\mu}{\sigma}
]

Here, ({I}_{3}) embodies the standardized pixel values. With all images normalized and standardized, the next critical step involves segmentation, aimed at isolating the region of interest (ROI), specifically cancer-affected areas such as nuclei and other pathological structures.

Image Segmentation

In the current methodology, Otsu’s thresholding method is implemented for segmentation. This technique effectively identifies the optimal threshold, reducing intra-class variance between foreground (cancerous regions) and background. The thresholding process is represented mathematically as:

[
T={arg}\,\max\left({\sigma}^{2}(\theta)\right)
]

Ultimately, the segmentation process can be summarized as:

[
{I}_{4}=\begin{cases} 1 & \text{if } I > T \ 0 & \text{if } I \leq T\end{cases}
]

Here, ({I}_{4}) represents the binary segmented image. With preprocessing successfully completed, the model proceeds to incorporate EfficientNetV2 for feature extraction.

EfficientNetV2 for Feature Extraction

Upon acquiring the preprocessed image ({I}_{4}), the model harnesses EfficientNetV2 for the extraction of features. EfficientNetV2 implements a compound scaling technique that systematically adjusts the network’s depth, width, and input resolution to optimize accuracy and computational efficiency.

The input image is processed through multiple layers, capturing both high-level features and low-level textures. Entailing an initial convolutional transformation, the process can be mathematically outlined as:

[
{F}{1}={\sigma}\left({W}{1}*{I}{3}+{b}{1}\right)
]

In this equation, ({F}{1}) denotes the feature map resulting from the first convolution operation, with ({W}{1}) representing the convolutional kernel and ({b}_{1}) indicating a bias term.

Mobile Inverted Bottleneck Convolutions

EfficientNetV2 utilizes several Mobile Inverted Bottleneck Convolution (MBConv) blocks, designed with the aim of conserving computational resources while maintaining feature integrity. The mathematical representation of an MBConv block can be formatted as:

[
{F}{i}={\sigma}\left({W}{d}\circ{F}{i-1}+{b}{d}\right)
]

Here, ({F}{i}) is the output of the (i^{th}) MBConv block, and ({W}{d}) denotes the depthwise convolution kernel. The efficiency of these blocks arises from their ability to separate spatial and channel-wise operations during convolution.

Through the progression of the input through successive layers, the network’s depth and the channel quantity of feature maps gradually augment, regulated by a compound scaling factor. The mathematical representation of the feature map at the (n^{th}) layer is denoted as:

[
{F}{n}=MBConv({F}{n-1})\in\mathbb{R}^{{H}{n}\times{W}{n}\times{C}_{n}}
]

Following this intensive feature extraction phase, a global operation is applied to further compress the feature map, making it suitable for sequential learning.

Global Average Pooling

The global average pooling operation takes the average value across spatial dimensions, represented mathematically as:

[
{F}{pooled}=\frac{1}{{H}{f}{W}{f}} \sum{i=1}^{{H}{f}}\sum{j=1}^{{W}{f}}{F}{final,ij}
]

This results in a feature vector of size ({D}_{f}), where each element signifies the averaged value for each channel across spatial dimensions.

Reshaping for GRU

To prepare for sequence learning with a Gated Recurrent Unit (GRU) supported by an attention mechanism, the feature vector must be reshaped. The feature map, typically in the form of a tensor ((H \times W \times C)), is flattened into a two-dimensional matrix ((T \times C)) where (T = H \times W).

This arrangement allows the GRU to interpret the spatial data of the image as a sequence, with each sequence step corresponding to distinct image regions.

Gated Recurrent Unit (GRU) for Sequential Learning

The extracted feature vector ({F}{pooled}) harbors significant information pertaining to the input image. In order to tap into the sequential dependencies within these features, the model employs a GRU. Initially, ({F}{pooled}) is reshaped into a sequence format for processing through GRU layers.

The input sequence can be represented as:

[
{F}{seq}\in\mathbb{R}^{L\times{D}{f}}
]

Here, (L) represents the length of the sequence, and ({D}_{f}) signifies the quantity of features for each unit in the sequence.

GRU Mechanisms

The GRU maintains a hidden state ({h}{t}) that is updated at every step by considering the current input and the preceding hidden state. The reset gate ({r}{t}) guides how much prior information should be retained, mathematically expressed as:

[
{r}{t}=\sigma\left({W}{r}\cdot\left[{h}{t-1},{F}{seq,t}\right]+{b}_{r}\right)
]

Likewise, the update gate ({z}_{t}) determines the extent to which previous information should be forwarded:

[
{z}{t}={\sigma}\left({W}{z}\cdot\left[{h}{t-1},{F}{seq,t}\right]+{b}_{z}\right)
]

The candidate activation (\tilde{h}_{t}) computes a new hidden state based on both the reset gate’s output and current input, represented as:

[
\tilde{h}{t}=\text{tanh}\left({W}{h}\cdot\left[{r}{t}\circ{h}{t-1},{F}{seq,t}\right]+{b}{h}\right)
]

The current hidden state ({h}_{t}) is a combination of the candidate state and the previous hidden state, weighted by the update gate:

[
{h}{t}=\left(1-{z}{t}\right)\circ{h}{t-1}+{z}{t}\circ\tilde{h}_{t}
]

This framework ensures that the GRU effectively captures temporal dependencies and relationships, thereby enriching its understanding of the processed sequences.

The Role of Attention Mechanism

Integrated within the GRU architecture is the attention mechanism, enhancing interpretability. For each time step, an attention score is computed to assess the significance of specific regions within the input sequence. The raw attention score for time step (t) can be calculated as:

[
{e}{t}=\text{tanh}\left({W}{e}\cdot{h}{t}+{b}{e}\right)
]

Following the calculation of attention scores for each hidden state, these scores are transformed into attention weights (\alpha_{t}) via the SoftMax function:

[
\alpha{t}=\frac{\text{exp}\left({e}{t}\right)}{\sum{k=1}^{L}\text{exp}\left({e}{k}\right)}
]

The context vector (c) is derived from the weighted sum of the hidden states:

[
c=\sum{t=1}^{L}\alpha{t}h_{t}
]

This context vector consolidates crucial information from the entire sequence, providing an enhanced focus on important regions while diminishing the less informative areas.

Classification Layer

After deriving the context vector (c), the classification layer is responsible for determining whether the tissue is benign or malignant. This classification layer processes (c) to generate scores for each class:

[
z={W}{c}\cdot c + b{c}
]

These scores are transformed into a probability distribution through the SoftMax function:

[
\hat{y}{k}=\frac{\text{exp}(z{k})}{\sum{i=1}^{K}\text{exp}(z{i})}
]

The resulting output (\hat{y}) contains probabilities for each class, allowing for a clear decision-making process regarding the classification of the breast tissue.

Loss Function and Training

To evaluate the model’s accuracy, a binary cross-entropy loss function is employed:

[
L=-\left[y\log(\hat{y}{1})+(1-y)\log(\hat{y}{0})\right]
]

The training process adopts an optimization strategy, utilizing the Adam optimizer to adjust model parameters iteratively, thereby minimizing the loss function through adaptive learning rates.

This detailed discourse on preprocessing, feature extraction, sequential modeling, and classification underscores the intricate methodologies employed in the proposed model for breast cancer detection using deep learning techniques. With each component strategically designed, the model aims to enhance diagnostic accuracy while providing interpretability in medical imaging analysis.