The Multi-Attribute Evaluation Model (MAEM) for Physical Education

In the world of education, especially in physical education, understanding student development requires a holistic approach. Enter the Multi-Attribute Evaluation Model (MAEM), a data-driven framework designed to compute a comprehensive evaluation score for students by considering various aspects of their development using artificial intelligence and deep learning algorithms. This article delves into how the MAEM operates, from its foundational stages to its practical implementation.

Problem Definition and Framework Design

At the core of MAEM is the pursuit of a holistic evaluation score—referred to as SSS—for each student, combining multiple attributes that signify diverse aspects of student growth. This holistic score is calculated using the equation:

$$
{H}{e} = \sum{j=1}^{N} {W}{j} {S}{j,j}
$$

Where:

• ( {H}_{e} ): Represents the holistic evaluation score for student ( e ),
• ( N ): Denotes the number of attributes encompassing physical, cognitive, emotional, and social development, among others,
• ( {W}_{j} ): The weight assigned to each attribute, reflecting its significance in the overall evaluation,
• ( {S}_{j,j} ): The score corresponding to the ( j )-th attribute for student ( e ).

This equation effectively combines various attributes into a singular comprehensive score, allowing educators to understand each student’s multifaceted growth better.

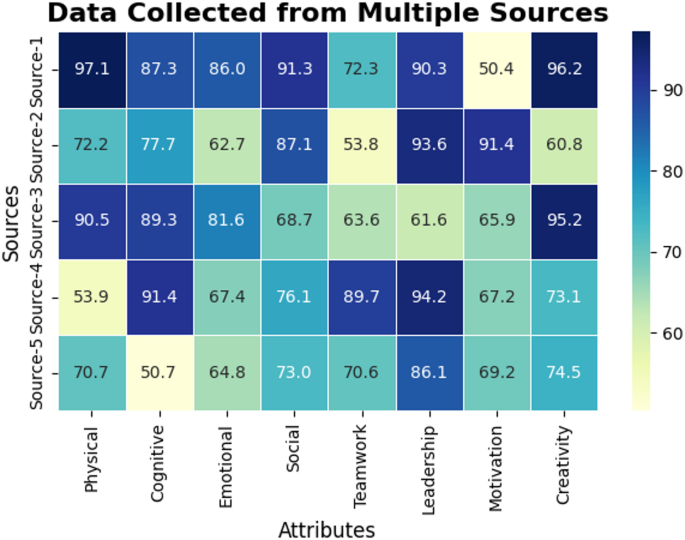
Data Collection

The implementation of the MAEM begins with robust data collection, where diverse sources come together to form a unified dataset. The dataset ( Y ) is encapsulated in the following equation:

$$
Y = \bigcup{i=1}^{M} {Y}{i}
$$

Where:

• ( M ): Represents the number of data sources, which might include surveys, tests, and external assessments,
• ( {Y}_{i} ): Data from the ( i )-th source.

The integration of these varied data sources allows for a more balanced and comprehensive assessment of each student’s attributes.

To ensure the reliability of evaluations, if multiple scores exist for the same attribute, they are averaged using the equation:

$$
{Q}{m,k} = \frac{1}{M} \sum{i=1}^{M} {Q}_{m,k}^{i}
$$

This ensures that the evaluations are rounded off, averting biases from any single source and reinforcing the accuracy of the assessment.

Preprocessing and Feature Engineering

An essential phase of data preparation involves addressing missing values. For numerical attributes, missing values are filled with the mean, defined by:

$$
{y}{m,n} = \frac{\sum{i=1}^{M}{N}{i,n} \cdot {y}{i,n}}{\sum{i=1}^{M}{N}{i,n}}
$$

Where:

• ( {y}_{m,n} ): The filled value for the ( n )-th attribute of student ( m ),
• ( {N}_{i,n} ): A binary mask indicating the presence of the ( i )-th value (where 0 represents missing).

Utilizing these imputation techniques helps ensure that no vital information gets discarded during preprocessing.

For categorical attributes, filling methods employ the mode. It helps in maintaining the integrity of the dataset, as shown in the visual representation of missing values per attribute from the data (refer to Fig. 2).

Normalization

Following the handling of missing values, the next step involves normalizing numerical features to the [0, 1] range using the equation:

$$
{\widehat{y}}{m,n} = \frac{{y}{m,n} – \text{min}({y}{n})}{\text{max}({y}{n}) – \text{min}({y}_{n})}
$$

Normalizing data is pivotal for ensuring comparability amongst different attributes, promoting fairness in evaluation.

Feature Extraction

A significant element in understanding the relationships among various student attributes involves feature extraction. New features are derived from existing attributes, for instance:

$$
Leadership_Teamwork = \frac{(Leadership + Teamwork)}{2}
$$

Such derived attributes effectively capture the interplay between various dimensions of student development and offer valuable insights into performance trends.

Development of Deep Learning Models

With preprocess and feature engineering complete, educators can now deploy deep learning models to process gathered data. These models utilize unified architectures that cater to both categorical and numerical inputs.

Input Representation

The architecture begins with normalized numerical and one-hot encoded categorical data, processed through activation functions which allow the model to unveil intricate, non-linear relationships.

Model Structure

The model’s structure integrates the equations:

$$
L{nni} = \text{ReLU}(X{nni} Y{nni} + a{nni})
$$

and

$$
L{ohe} = \text{ReLU}(X{ohe} Y{ohe} + a{ohe})
$$

These equations demonstrate how inputs are initially processed through ReLU activation functions.

The outputs from numerical and categorical inputs are then combined and passed through dense layers:

$$
L = \text{ReLU}(X{oa}[L{nni}:L{ohe}] + a{oa})
$$

This design allows for the exploration of interactions among different data types, resulting in more informed score predictions.

Output Prediction

The final output layer uses the softmax function to convert raw outputs into a probability distribution, yielding a holistic score calculated through:

$$
O = \text{Softmax}(X{oa}L + a{oa})
$$

This process aids in predicting the overall score of every student, fostering a deeper understanding of their developmental status.

Multi-Attribute Scoring and Assessment

Scores are synthesized through weighted sums, incorporating attributes according to their respective significances in a student’s assessment:

$$
{H}{e} = \sum{j=1}^{N}{W}{j} {\widehat{S}}{i,j}
$$

This aggregated approach facilitates a well-rounded depiction of each individual’s growth trajectory.

Feedback Mechanism

An integral aspect of MAEM is its feedback mechanism. By calculating gaps between target and actual scores, educators can pinpoint areas in need of improvement:

$$
{D}{m,j} = {P}{j} – {\widehat{S}}_{m,j}
$$

Through this feedback, actionable insights are generated, enabling tailored strategies for each student.

Pilot Testing and Model Validation

To ensure reliability, the MAEM must undergo rigorous pilot testing and validation. Key metrics such as Mean Absolute Error (E) and Coefficient of Determination ((R^2)) are used to evaluate the model’s performance:

$$
E = \frac{1}{M} \left(\sum{m=1}^{M} |{A}{m} – {P}_{m}|\right)
$$

and

$$
{R}^2 = 1 – \frac{\sum{m=1}^{M} ({P}{m} – A{m})^{2}}{\sum{m=1}^{M} ({P}_{m} – \overline{P})^{2}}
$$

These metrics provide tangible performance insights, ensuring the model can accurately forecast students’ scores.

Monitoring and Continuous Improvement

An effective evaluation process necessitates ongoing monitoring and constant improvement to adapt to changing educational landscapes.

Drift Detection

Drift detection measures shifts in feature distributions over time using metrics like Kullback-Leibler (KL) divergence:

$$
E(O||R) = \sum_{j} O(j) \log \frac{O(j)}{R(j)}
$$

By keeping track of feature distribution changes, educators can identify potential data drifts that may skew model predictions.

Retraining

Establishing retraining triggers is essential for maintaining robust performance. For instance:

$$
Trigger\;Retraining\;if\;R^{2} < th
$$

This condition ensures that the model is regularly updated to reflect the latest educational dynamics, affirming its relevance and effectiveness.

By implementing MAEM, educational institutions can aspire to achieve a comprehensive understanding of student development across multiple dimensions, thus fostering a supportive environment for personal and academic growth. The journey from data collection through to continuous improvement encapsulates an integrated methodology that thrives on informed decision-making and dynamic adaptation.