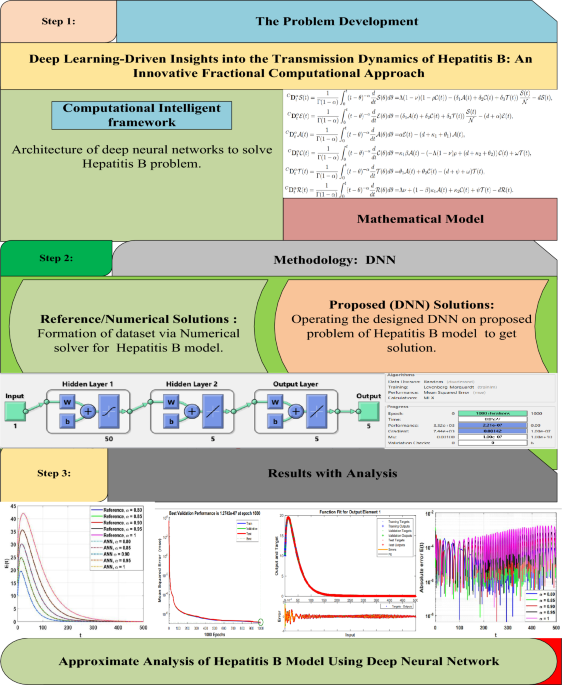
An In-Depth Analysis of the Caputo HBV Model (2): Steady State and Stability

The Caputo HBV model (2) offers a comprehensive framework for understanding the dynamics of the Hepatitis B virus. This article provides a detailed exploration of the model’s equilibria, specifically its endemic and disease-free equilibria, as well as an evaluation of its local stability.

Model Equilibria

The foundational aspect of analyzing any epidemiological model lies in its equilibria, which in the case of the Caputo HBV model (2), can be described through two key types: the endemic equilibrium ((\mathcal{D}_1)) and the disease-free equilibrium ((\mathcal{D}_0)).

Endemic Equilibrium ((\mathcal{D}_1))

The endemic equilibrium represents a state where the disease persists in the population. It is expressed as:
$$\mathcal{D}_1 = \left( \mathcal{S}^{}, \mathcal{E}^{}, \mathcal{A}^{}, \mathcal{C}^{}, \mathcal{T}^{}, \mathcal{R}^{} \right),$$
where each variable corresponds to specific compartments of the model:

• S: Susceptible individuals
• E: Exposed individuals
• A: Asymptomatic individuals
• C: Chronic individuals
• T: Treated individuals
• R: Recovered individuals

The dynamic interactions among these compartments are governed by the following system of equations:

• $$\mathcal{S}^{} = \frac{W_1 \mathcal{E}^{} \mathcal{N}^{}}{\delta_1 \mathcal{A}^{} + \delta_2 \mathcal{C}^{} + \delta_3 \mathcal{T}^{}}$$
• $$\mathcal{E}^{} = \frac{W_2 \mathcal{A}^{}}{\xi}$$
• $$\mathcal{C}^{} = \frac{\beta \kappa_1 \mathcal{A}^{} + \omega \mathcal{T}^{**}}{W_3}$$
• $$\mathcal{T}^{} = \frac{\theta_1 \mathcal{A}^{} + \theta_2 \mathcal{C}^{**}}{W_4}$$
• $$\mathcal{R}^{} = \frac{\kappa_1(1-\beta) \mathcal{A}^{} + \kappa_2 \mathcal{C}^{} + \nu \Lambda + \psi \mathcal{T}^{}}{d}$$

Integrating these relations leads to a critical expression for (\mathcal{A}^{}):
$$\mathcal{A}^{} = \frac{\xi \Lambda \omega \left( W_3 W_4 – \theta_2 \omega \right)^2 W_1 W_2\left( \mathcal{R}_0 – 1 \right)}{a_1 + a_2 + a_3 + a_4}.$$

Disease-Free Equilibrium ((\mathcal{D}_0))

In contrast, the disease-free equilibrium indicates a state where the disease is absent in the population:
$$\mathcal{D}_0 = \left( \frac{\Lambda(1-\nu)}{d}, 0, 0, 0, 0, \frac{\Lambda \nu}{d} \right).$$

It provides a baseline to assess the stability of the model, particularly when evaluating the effectiveness of interventions in controlling the outbreak of HBV.

Basic Reproduction Number (\mathcal{R}_0)

The basic reproduction number, (\mathcal{R}_0), is a pivotal parameter in understanding the epidemic potential of the disease. It is calculated using a next-generation method, which involves evaluating certain matrices ((F) and (V)):

• $$F = \begin{pmatrix}
  0 & (1-\nu)\delta_1 & (1-\nu)\delta_2 & (1-\nu)\delta_3 \
  0 & 0 & 0 & 0 \
  0 & 0 & 0 & 0 \
  0 & 0 & 0 & 0
  \end{pmatrix}$$

• $$V = \begin{pmatrix}
  W_1 & 0 & 0 & 0 \
  -\xi & W_2 & 0 & 0 \
  0 & -\beta \kappa_1 & W_3 & -\omega \
  0 & -\theta_1 & -\theta_2 & W_4
  \end{pmatrix}$$

From this, we compute (\mathcal{R}_0) using:
$$\mathcal{R}_0 = \frac{\xi(1-\nu) \left( \theta_1 \left( \delta_2 \omega + \delta_3 W_3 \right) + \delta_1 \left( W_3 W_4 – \theta_2 \omega \right) + \beta \kappa_1 \left( \delta_3 \theta_2 + \delta_2 W_4 \right) \right)}{W_1 W_2 \left( W_3 W_4 – \theta_2 \omega \right)}.$$

Local Stability Analysis

The stability of the HBV treatment model is evaluated through the following theorems:

Theorem 1

The disease-free equilibrium (\mathcal{D}_0) is locally asymptotically stable if the argument of all roots ((\lambda)) of the characteristic equation satisfies the condition:
$$|\arg(\lambda)| > \frac{\pi}{2 \mathcal{L}},$$
where (\mathcal{L}) is defined based on the Jacobian matrix.

Theorem 2

The model is locally asymptotically stable at (\mathcal{D}_0) if (\mathcal{R}_0 < 1). Conversely, it becomes unstable when (\mathcal{R}_0 \geq 1).

Existence and Uniqueness of Solutions

To establish the existence and uniqueness of solutions for the Caputo HBV model, we can formulate it in a concise manner:
$$
^C\bf{D}_t^\alpha \mathcal{S}(t) = n_1(t, \mathcal{S}, \mathcal{E}, \mathcal{A}, \mathcal{C}, \mathcal{T}, \mathcal{R}),
$$
and other equations for (\mathcal{E}, \mathcal{A}, \mathcal{C}, \mathcal{T}, \mathcal{R}).

Analysis reveals that continuity in the partial derivatives incurs existence and uniqueness:

• The derivatives of (n_i) with respect to each compartment demonstrate continuity within a defined region in (\mathbb{R}^2).

As such, a unique continuous vector solution exists for a specified interval.

Global Stability via Hyers–Ulam–Rassias Stability

A notable aspect of global stability involves utilizing the Hyers–Ulam–Rassias framework. This methodology scrutinizes if approximate solutions remain sufficiently close to exact solutions under specific conditions. The model can be represented as:
$$
^C\bf{D}_t^\alpha[\Psi(t)] = \Omega(t, \Psi(t)),
$$
with the stability defined through constant inequalities that bind deviation from exact solutions.

This examination paves the way to assert that if certain conditions are met (continuity, boundedness of solutions), the Caputo HBV model exhibits generalized Hyers–Ulam–Rassias stability across defined intervals.

In sum, the Caputo HBV model (2) not only provides insight into the dynamics of hepatitis B but also establishes a robust mathematical foundation for the assessment of disease management strategies through its analysis of equilibria, steady states, and stability conditions.