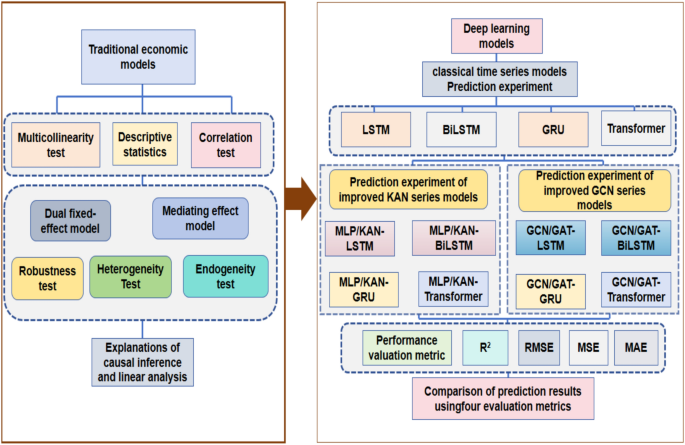
Benchmarking Time Series Models: Evaluating KAN and GNN Frameworks

Introduction

In the realm of time series forecasting, selecting the optimal model is crucial to capturing intricate patterns within data. This chapter delves into experimental analyses of four benchmark time series models, laying the groundwork for a comprehensive examination of model performance. It starts by discussing foundational models—Long Short-Term Memory (LSTM), Bidirectional LSTM (BiLSTM), Gated Recurrent Unit (GRU), and Transformers—before presenting advanced methodologies reinforced by Kolmogorov-Arnold Networks (KAN) and Graph Neural Networks (GNNs).

Overview of Four Classical Time Series Models

Classical Models: A Brief Intro

The traditional models under scrutiny are essential for establishing a baseline for further experimentation. Each model possesses distinctive attributes that inform its forecasting ability. For instance, LSTMs are adept at managing long-range dependencies, making them ideal for sequences with significant temporal structures. BiLSTMs enhance this capability by processing sequences in both forward and backward directions, while GRUs simplify the LSTM architecture for efficiency. Transformers revolutionize the field through self-attention mechanisms, eliminating the limitations associated with sequential data processing.

Analysis of Nonlinear Relationships

The focus on the nonlinear dynamics between the dependent variable (DIF) and other features (TFPLP) is critical. By implementing KAN, GCN, and GAT, the chapter aims to uncover deeper dynamics beyond linear assumptions, improving predictive accuracy and model interpretability.

Experimental Methods and Data

Overall Experimental Design

Diving into the experimental design, the enhancement of traditional time series models with KAN and GNNs reflects a structured approach to improving accuracy and generalization. The KAN network augments LSTM, BiLSTM, GRU, and Transformer models by substituting the MLP layer, while GCN and GAT extract high-dimensional features, thus forming hybrid frameworks. Employing a five-fold cross-validation with a robust training/testing split ensures a reliable assessment of model performance.

Data Preparation

Data preparation is integral, encompassing steps of cleaning, denoising, and standardizing time series data. Missing values are addressed through interpolation or mean imputation, while outliers are tackled using Z-scores. Following preprocessing, the dataset is split into training and testing sets to ensure the majority of the data aids in the learning process.

Comparative Framework: KAN and GNNs

The KAN Framework

KAN models, grounded in the Kolmogorov-Arnold representation theorem, enable the approximation of multivariable continuous functions through a superposition of univariate functions. By enhancing traditional MLP architectures, KAN captures complex relationships in a simplified manner.

GNNs and Their Advantages

Graph Convolutional Networks (GCNs) and Graph Attention Networks (GATs) add another layer of sophistication. GCNs focus on aggregating information across nodes, while GATs leverage attention mechanisms that dynamically adjust weights based on node importance. This flexibility allows for a deeper exploration of relationships within time series data, particularly in economic contexts.

Performance Valuation Metrics

A reliable evaluation of model performance relies on several standardized metrics, including R², RMSE, MSE, and MAE. Each metric serves a distinct purpose:

1. R² (Coefficient of Determination) gauges the proportion of variance captured by the model.
2. RMSE (Root Mean Square Error) assesses how well the model generalizes to unseen data.
3. MSE (Mean Square Error) highlights the overall prediction error.
4. MAE (Mean Absolute Error) provides an average of the absolute errors, offering insights into prediction accuracy.

Employing these metrics ensures a well-rounded assessment of each model’s efficacy in forecasting tasks.

The Enhanced Framework Based on KAN

KAN vs. MLP

The comparison between KAN and traditional MLP showcases notable advancements. KAN’s architecture minimizes redundant connections and optimizes representation efficiency while retaining the ability to approximate any continuous function.

Hyperparameter Optimization in KAN Models

During hyperparameter tuning, dynamic adjustments occur based on performance feedback, amplifying the models’ predictive capacities. Learning rates, hidden layer dimensions, and dropout rates are systematically modified to optimize learning stability.

Comparative Ablation Studies

Ablation studies present compelling insights into the impact of KAN compared to MLP architectures across various models, consistently showing that KAN enhances performance, albeit with increased computational overhead.

GNNs: Enhancing Traditional Models

GCN and GAT Frameworks

The incorporation of GCN and GAT into traditional time series models marks an evolution in the approach to forecasting. GCN leverages adjacency matrices to capture dependencies in graph structures, while GAT adapts attention mechanisms for nuanced insights.

Performance Trade-offs

While both GCN and GAT models exhibit significant improvements in prediction accuracy, they also incur higher computational costs. Balancing these factors is crucial in practical applications where efficiency is necessary.

Statistical Analysis Framework

Employing rigorous statistical analyses through paired t-tests, effect size calculations, and estimating MAE across models comprehensively evaluates the performance improvements wrought by KAN and GNN enhancements. This multivariate analytical approach solidifies the credibility of the model assessments.

Closing Thoughts on Model Performance

As emerging frameworks like KAN and GNN technologies redefine traditional forecasting methods, understanding their contributions through structured analyses is pivotal. This chapter provides the foundation for subsequent discussions on model efficacy, paving the way for advanced interpretations and applications in time series forecasting.