The BB84 Protocol: A Deep Dive into Quantum Key Distribution

Introduction to the BB84 Protocol

The BB84 protocol, proposed in 1984 by Charles Bennett and Gilles Brassard, revolutionized secure communication. This groundbreaking quantum key distribution (QKD) method allows two parties—traditionally referred to as Alice and Bob—to generate and distribute a secure classical binary key over a quantum channel. Notably, the protocol requires a verified and authenticated classical channel to ensure security against potential eavesdroppers, often called Eve.

What sets the BB84 protocol apart is its reliance on the fundamental laws of physics, such as the no-cloning theorem, which prevents an eavesdropper from perfectly replicating quantum states. This capability guarantees that Alice and Bob can securely communicate, even in the presence of an adversary.

Key Steps in Establishing a Secure Connection

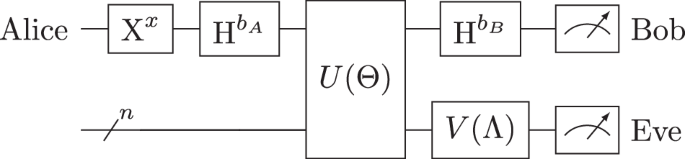
The process of generating a shared secret key between Alice and Bob consists of several well-defined steps:

1. State Preparation

Alice begins by randomly selecting a bit value ( x \in {0, 1} ) and another random bit ( b_A \in {0, 1} ) that dictates the orthogonal bases used for encoding the bit. The bases used are the ( Z )-basis (when ( b_A = 0 )) or ( X )-basis (when ( b_A = 1 )).

• If ( x = 0 ) and ( b_A = 0 ): The prepared qubit is ( |0\rangle )
• If ( x = 0 ) and ( b_A = 1 ): The prepared qubit is ( |+\rangle )
• If ( x = 1 ) and ( b_A = 0 ): The prepared qubit is ( |1\rangle )
• If ( x = 1 ) and ( b_A = 1 ): The prepared qubit is ( |-\rangle )

2. Transmission

Once the qubits are prepared, Alice transmits them to Bob through the quantum channel, where the properties of quantum mechanics come into play.

3. Measuring

Bob, upon receiving the qubits, similarly selects a basis to measure the received quantum states. He chooses ( b_B \in {0, 1} ) for his measurement basis, either ( Z ) or ( X ).

4. Sifting

After measurement, Alice and Bob reveal their basis choice over the classical channel. If ( b_A = b_B ), the bit measured by Bob becomes part of their raw key. Otherwise, the bit is discarded. Sifting can be performed after each individual bit or collectively for a block of bits.

In an ideal scenario, Alice and Bob would always have identical raw keys. However, real-world imperfections introduce errors, requiring additional steps for error reconciliation and privacy amplification to secure their shared key.

Post-processing Steps

To reconcile their keys, Alice and Bob need to communicate using the authenticated classical channel. They can use protocols like Cascade or Low-Density Parity-Check codes for error reconciliation. However, sharing this information can give Eve some insights into their raw keys, highlighting the need for effective privacy amplification techniques to ensure that Eve cannot gain access to the final reconciled key.

Privacy Amplification

This essential process distills the reconciled key to eliminate any information that an adversary might glean from the errors, further strengthening the security of their communication.

Attacks on the BB84 Protocol

The BB84 protocol is not immune to attacks, and two prominent categories exist:

Individual Attacks

In individual attacks, Eve uses the same quantum circuit for each qubit transmission. Here, her strategy is independent for each qubit, meaning she does not accumulate information from the earlier bits in the sequence.

Example of Individual Attack

An example of such an attack might involve Eve using a quantum circuit to interact with the quantum channel during transmission. For instance, Eve might delay a unitary operation until classical information is exchanged between Alice and Bob. This approach allows her to optimize her measurements based on the shared basis information.

Collective Attacks

Collective attacks are generally more powerful. In this variant, Eve uses a consistent quantum circuit for each qubit but her measurements might depend on the entire sequence of qubits transmitted, making her attack more nuanced and potentially more successful.

Eve could store the approximate copies of the qubits sent by Alice and utilize the shared classical information during reconciliation to optimize her measurement strategy, creating a stronger position for any potential interception.

Optimal Individual Attacks

The security of the BB84 protocol heavily relies on the no-cloning theorem. This principle ensures that even the most sophisticated attacks can only produce approximate clones of quantum states.

Phase Covariant Cloning Machines (PCCMs) represent the optimal strategy for implementing these types of attacks. For example, if the transmission channel is error-free, Eve can use PCCMs to maximize her chances of successfully predicting Alice’s bits.

Measuring Eve’s Success Rates

Eve’s fidelity in measuring Alice’s qubits is defined in terms of her attack’s success in accurately determining the bits. The equation below calculates the fidelity of her attack:

[
F(\rho_A,\rho_B) = \left(\text{Tr}\sqrt{\sqrt{\rho_A} \rho_B \sqrt{\rho_A}}\right)^2
]

Where (\rho_A) is Alice’s density matrix and (\rho_B) represents Bob’s matrix following Eve’s attack.

QCL: Quantum Circuit Learning in Attacks

Quantum Circuit Learning (QCL) provides a framework for optimizing attacks on the BB84 protocol. Using a parametrized quantum circuit, Eve can adapt her attack strategy based on the continuous flow of information and the specifics of the transmission.

Optimizing QCL Attacks

Eve can implement a quantum circuit capable of learning optimal attack configurations using gradient descent methods, leveraging multiple parameters to navigate the complex landscape of potential attacks on the key exchange.

Noisy Channels and Alternate Strategies

Real-world quantum channels often have noise, which can provide additional challenges to secure communication. This noise might stem from environmental factors or intentional error introduction for robustness.

QCL can still optimize Eve’s attacks in the presence of noise, allowing her to achieve superior fidelity in distinguishing between Alice’s sent states. The ability to adapt and optimize using QCL can yield significant advantages in practical scenarios.

Exploring Imbalanced Cloners

The introduction of imbalanced cloners highlights how different types of noise can alter Eve’s strategies. By adjusting the circuit parameters based on specific noise characteristics, Eve can significantly increase her chances of success, potentially outperforming traditional methods like the PCCM.

Collective Attacks: An Advanced Strategy

In a collective attack, Eve utilizes her quantum memory to create a more intricate and responsive strategy. By employing her cloned states more effectively and optimizing her approach through QCL, she can distinguish between different qubits with improved success rates.

Analysis of Collective Attacks

For example, when Alice and Bob share a key of minimal length, even small changes in basis choice can have substantial implications for security. Eve can craftily leverage parity information from the shared key to execute optimized measurements on her quantum memory, thus increasing the likelihood of correctly deducing the exchanged bits.

Concluding Thoughts

The BB84 protocol presents a robust framework for quantum key distribution, but its effectiveness hinges on understanding the intricate balance of state preparation, transmission, measurement, and post-processing steps. By recognizing potential attack vectors and implementing QCL strategies for optimization, both Alice and Bob can fortify their communication against potential eavesdropping, while threats like individual and collective attacks continue to challenge the landscape of quantum cryptography.