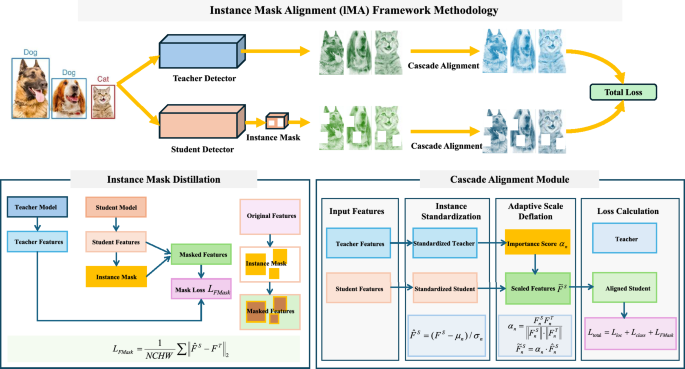
Instance Mask Alignment (IMA) Framework for Object Detection Knowledge Distillation
Introduction
In the rapidly evolving field of computer vision, object detection is a critical task that involves identifying and classifying multiple objects within an image. To enhance the efficiency and effectiveness of object detection models, the concept of knowledge distillation has emerged as a valuable technique. In this article, we delve into our proposed Instance Mask Alignment (IMA) framework, designed specifically for knowledge distillation in object detection. We will revisit traditional approaches and introduce key components of the IMA framework, detailing the innovative principles behind it.
Revisiting Object Detection Knowledge Distillation
Before exploring the IMA framework, it’s essential to understand conventional knowledge distillation methods used in object detection. Typically, these methods focus on training a smaller, student model (S) to replicate the behavior of a larger, pre-trained teacher model (T). The objective is to optimize the feature distillation loss, encouraging the student to mimic the teacher’s intermediate features.
Mathematically, the middle-level features of both models can be represented as (F^S \in {\mathbb{R}}^{N \times C \times H \times W}) for the student and (F^T \in {\mathbb{R}}^{N \times C \times H \times W}) for the teacher, where (N) is the number of instances, (C) the number of channels, and (H) and (W) the spatial dimensions of the feature maps. The feature distillation loss (L_{KD}) is then given by:
[
L{KD} = \frac{1}{NCHW} \sum{n=1}^{N}\sum{k=1}^{C}\sum{i=1}^{H}\sum{j=1}^{W}{\mathcal{D}}{f}(F{n,k,i,j}^{T} – f{align}(F_{n,k,i,j}^{S}))
]
Here, ({\mathcal{D}}{f}(\cdot)) measures the difference between features from the teacher and student. The adaptation layer (f{align}) aligns the student’s features with the teacher’s, thereby allowing the student model to learn comparable intermediate representations.
Instance Mask Distillation
Building on this foundation, we introduce our Instance Mask Distillation module, aimed at enhancing the transfer of spatial information at the instance level. This innovative module employs instance masks to guide the student model, ensuring it focuses on regions of interest within the input data, ultimately improving detection accuracy.
The module works by generating a binary mask (M \in {\mathbb{R}}^{H \times W \times 1}) with a random mask ratio (\zeta \in [0, 1)), which is defined as follows:
[
M{i,j} = \begin{cases}
0, & R{i,j} < \zeta \
1, & R_{i,j} \ge \zeta
\end{cases}
]
Here, (R_{i,j}) is sampled from a uniform distribution ({\mathcal{U}}(0,1)). The masked output of the student model’s features is computed as:
[
\hat{F}^S = {\mathcal{F}}^{-1}(M \odot {\mathcal{F}}(F^S))
]
Subsequently, we derive the knowledge distillation loss (L_{FMask}) as the mean squared error between the masked student features and the teacher features:
[
L{FMask} = \frac{1}{NCHW} \sum{n=1}^{N}\sum{k=1}^{C}\sum{i=1}^{H}\sum{j=1}^{W} \left\Vert \hat{F}^S{n,k,i,j} – F^T_{n,k,i,j} \right\Vert_2
]
By focusing on specific, masked regions, the student model receives targeted guidance from the teacher’s instance masks, leading to a deeper understanding of the spatial boundaries of objects and better detection outcomes.
Cascade Alignment Module
To further enhance this distillation process, we propose the Cascade Alignment Module, which bridges the gap between different detector architectures, facilitating seamless knowledge transfer. This module comprises two integral components: Instance Standardization and Adaptive Scale Deflation.
Instance Standardization
Instance Standardization normalizes the instance-level features, combating internal covariate shift and improving training stability. Achieving this involves computing the mean (\mu_n) and standard deviation (\sigma_n) across the spatial dimensions for each instance (n):
[
\mun = \frac{1}{HW} \sum{i=1}^{H}\sum{j=1}^{W} F^S{n,c,i,j}
]
[
\sigman = \sqrt{\frac{1}{HW} \sum{i=1}^{H}\sum{j=1}^{W} (F^S{n,c,i,j} – \mu_n)^2}
]
The instance-level features are then standardized:
[
\hat{F}^S = \frac{F^S – \mu_n}{\sigma_n}
]
This normalization step is crucial for facilitating effective knowledge transfer, especially when working with varying detector architectures that may have significantly different feature distributions.
Adaptive Scale Deflation
Enhancing the results of Instance Standardization, the Adaptive Scale Deflation module adaptively scales the instance-level features according to their relevance. This allows the student model to prioritize the most informative instances while mitigating noise from irrelevant data.
For each instance (n), we compute an importance score (\alpha_n \in [0, 1]):
[
\alpha_n = \frac{F^S_n \cdot F^T_n}{\left\Vert F^S_n \right\Vert \left\Vert F^T_n \right\Vert }
]
Then, we apply the scaling factor (\gamma_n) to the standardized features:
[
\gamma_n = \alpha_n
]
[
\tilde{F}^S_n = \gamma_n \hat{F}^S_n
]
By cascading the Instance Standardization and Adaptive Scale Deflation modules, our framework ensures that the most relevant features are emphasized during the knowledge transfer process, thereby significantly enhancing detection performance.
Total Optimization and Inference
During the training phase, we jointly optimize the object detection loss along with the distillation losses introduced by our proposed modules. The total loss function is expressed as:
[
L{total} = L{loc} + L{cls} + L{FMask}
]
where (L{loc}) represents the localization loss, and (L{cls}) pertains to the classification loss. Each of these components is critical for refining the student model’s performance.
For the localization loss (L_{loc}), we measure the difference between the predicted bounding boxes and the ground truth using a smooth (L_1) loss:
[
L{loc} = \sum{i=1}^{N{pos}} \text{smooth}{L1}(b_i^{pred} – b_i^{gt})
]
The classification loss (L_{cls}) evaluates the accuracy of the predicted class probabilities against the ground truth:
[
L{cls} = -\sum{i=1}^{N{pos}} \sum{j=1}^{C} y{ij} \log(p{ij})
]
During inference, the student model generates object classification and localization information independently, without reliance on the teacher model or the distillation losses.
Theoretical Foundation of Instance Mask Alignment
The theoretical foundation of our IMA framework is predicated on the observation that conventional knowledge distillation methods often struggle with the structural differences that exist between various detector architectures. This challenge becomes particularly pronounced when comparing different detection paradigms such as two-stage versus one-stage or anchor-based versus anchor-free models.
An information-theoretic perspective reveals that optimizing the teacher-student knowledge transfer process can be significantly enhanced by focusing on the most informative regions within the feature maps, specifically the instance regions. By prioritizing these regions during the distillation process, we can effectively ensure that the knowledge transferred from the teacher to the student is directly relevant to the detection tasks at hand.
Additionally, it is observed that feature distributions across different detector architectures tend to vary considerably, even when trained on identical datasets for the same objectives. This distribution shift presents a substantial barrier to effective knowledge transfer, as it may lead to difficulties for the student model in accurately mimicking the feature representations of the teacher. To tackle this issue, we incorporate the principles of feature distribution alignment through instance standardization and adaptive scaling.
Formally, let (p_T(F)) and (p_S(F)) denote the probability distributions of the teacher’s and student’s feature maps, respectively. The goal is to minimize the divergence between these distributions:
[
\min_{S} D(p_T(F) || p_S(F))
]
In our framework, we simplify the challenge of directly minimizing this divergence by first transforming the feature maps via:
[
\min_{S} D(p_T(g(F)) || p_S(g(F)))
]
Here, (g(\cdot)) represents the cascade of instance standardization and adaptive scale deflation discussed earlier.
Pseudo-Code for the IMA Algorithm
To encapsulate the workings of our IMA framework, we present a structured pseudo-code that delineates the core algorithm. The steps cover the extraction of features from both the teacher and student models, the implementation of the Instance Mask Distillation module, followed by the Cascade Alignment Module’s application for each instance. The algorithm concludes with the computation of detection losses and the process of updating the student model by minimizing the total loss.
By employing the structured guidance of the IMA framework, we pave the way for a more efficient and effective approach to object detection knowledge distillation, offering a pathway toward improved model performance and robustness in real-world applications.