The Fourier-Based KAN Layer: A Game Changer in Neural Network Architecture

Introduction to Fourier-based KANs

In the realm of neural network architecture, the introduction of Kolmogorov–Arnold Networks (KANs) has set the stage for a significant paradigm shift. Drawing inspiration from the Kolmogorov–Arnold superposition theorem, KANs propose a compelling concept: any multivariate continuous function can be represented as a finite composition of univariate functions and additions. This foundation allows KANs to generalize Layer design by constructing each layer as a sum of learnable univariate functions, moving away from traditional fixed nonlinearities, such as ReLU. The implications? A more compact, accurate, and efficient way to approximate functions within machine learning frameworks.

The Transition to Fourier Series

In this exploration, we delve deeper into the evolution of KANs by adopting Fourier series as the backbone for pre-activation functions. This innovative step enhances the model’s capacity to encapsulate both low-frequency and high-frequency patterns, particularly in graphs. Where previous KAN formulations utilized B-spline functions, the Fourier series approach allows for smoother and more compact representations. This not only improves gradient flow but also amplifies parameter efficiency in our models.

Theoretical Underpinnings

The theoretical foundation supporting the Fourier-based KAN architecture is robust, resting on Carleson’s convergence theorem alongside Fefferman’s multivariate extension. These principles cultivate a strong approximation capability, confirming that our proposed architecture can effectively capture the intricacies of square-integrable multivariate functions. This rigor lends credence to the expressive power of our model and establishes strong theoretical guarantees for its application.

Theorem Overview

The foundational theorems posit that for any square-integrable function, there are adaptable Fourier-based KAN structures that can achieve an arbitrary level of accuracy to that function. As such, the incorporation of Fourier series enhances the KAN framework’s effectiveness in function representation, promising significant empirical advantages.

KA-GNNs: A New Class of Graph Neural Networks

Building on insights from Fourier-based KANs, we introduce KA-GNNs—Graph Neural Networks (GNNs) that integrate KAN modules throughout every GNN pipeline. This amalgamation substitutes conventional MLP transformations with dynamic Fourier-based layers, culminating in a unified architecture that is fully differentiable and boasts enhanced representational capabilities.

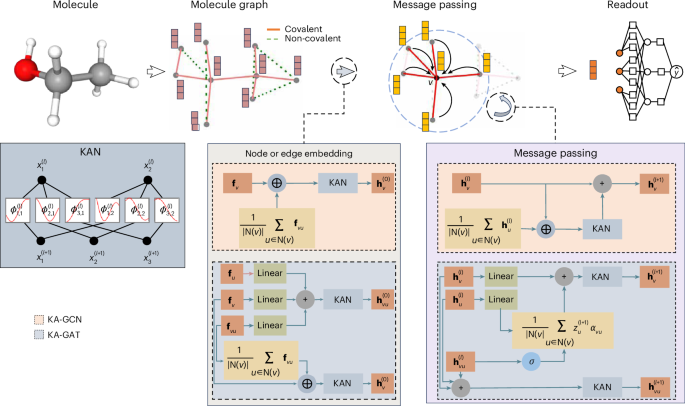
Designing KA-GCN and KA-GAT

Within the KA-GNN framework, two primary variants emerge: KA-GCN and KA-GAT. Each variant employs Fourier-based KAN modules to facilitate richer node embeddings and modulate feature interactions during message passing.

• KA-GCN computes initial node embeddings by combining atomic features (like atomic number and radius) and the average of neighboring bond features. This dual encapsulation employs data-driven trigonometric transformations to accurately represent atomic identity and local chemical context.

• KA-GAT, on the other hand, elevates the architecture by incorporating edge embeddings. By fusing edge features with those of endpoint atoms, KA-GAT constructs context-aware bond representations that enhance the GNN’s ability to capture complex interactions during message passing.

Application in Molecular Property Prediction

Transitioning our KA-GNN models to molecular data representation, we depict each molecule as a graph, where atoms serve as nodes and their interactions represent edges. This structure enables the model to leverage a comprehensive understanding of both local and long-range dependencies.

Features of Graph Representation

The input representation consists of atoms encoded with multifaceted vectors, encompassing characteristics like atomic number and electronegativity, while edges are similarly encoded based on their bond types. This meticulous graph construction equips KA-GNNs with the contextual nuances necessary for accurate molecular property predictions.

Evaluating KA-GNN Performance

Our empirical evaluations utilize seven benchmark datasets from MoleculeNet, allowing us to compare KA-GNNs against several state-of-the-art GDL models. When scrutinizing performance across various molecular datasets, our models stand out—especially on complex datasets such as ClinTox and MUV, showcasing impressive improvements in prediction accuracy.

Comparative Results

To ensure reliability, experimental settings were standardized across models, with detailed hyperparameter configurations disclosed. The results consistently affirm the superior effectiveness of KA-GNNs, particularly in capturing the complexities inherent in molecular data.

The Significance of Basis Functions in KA-GNNs

At the heart of our architecture lies the choice of basis functions. In comparing B-spline, polynomial, and Fourier series formulations, we find compelling evidence that Fourier-based KANs not only enhance prediction accuracy but also improve feature embedding processes and message-passing capabilities.

Efficiency of Fourier-based KANs

From an efficiency standpoint, Fourier-based KAN models demonstrate marked performance advantages compared to B-spline KANs and conventional MLP-based frameworks. The global nature of sinusoidal functions allows for a reduced parameter count, resulting in a more effective computational framework, especially in graph learning tasks.

Interpretability of KA-GAT

Beyond performance metrics, interpretability serves as a key pillar of the KA-GNN framework. Through a series of techniques, including saliency mapping, we can visualize how individual atoms and bonds contribute to model predictions, offering insights that align with chemical principles and enhancing the model’s transparency.

Analyzing Molecule Structures

In practical applications, we can analyze specific molecular structures, examining the influence of various functional groups on predictions. By developing subgraph representations that highlight critical components, KA-GNNs facilitate domain-relevant insights, proving invaluable in contexts such as drug discovery.

In summary, the Fourier-based KAN layer represents a significant leap forward in neural network architecture, marrying theoretical rigors with practical applications in molecular property predictions. Through effective integration into GNN frameworks like KA-GCN and KA-GAT, we can empower deeper insights into chemical interactions, marrying mathematics with science in unprecedented ways.