Introducing the OGFormer Model: Optimized Attention Scores for Graph Representation Learning
In the vast landscape of machine learning, graph-based data structures have grown tremendously in importance, especially in fields like social networks, recommendation systems, and biological networks. One of the latest innovations in processing such graph data is the OGFormer model, a sophisticated framework designed to optimize attention scores for improved graph representationlearning. This article presents a detailed exploration of the OGFormer model, which consists of three primary modules: Single-Head Self-Attention (SSA), Structural Encoding (SE), and a dedicated loss module for end-to-end optimization of attention scores.
Overview of the OGFormer Framework
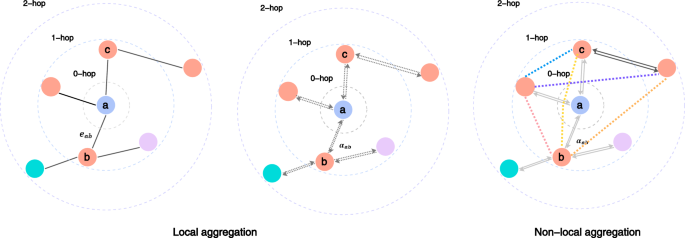
As illustrated in Figure 2, the OGFormer model reimagines traditional transformers to better suit the unique characteristics of graph data. In contrast to sequential data like text or image pixels, graph nodes are unordered and numerous, prompting a different approach to attention mechanisms. The goal of the OGFormer model is to effectively capture global dependencies between nodes while minimizing unnecessary computational expenses.
The OGFormer Layer
The OGFormer layer operates on node classification tasks within graphs, treating individual nodes as tokens. Given the unordered nature of graph nodes, the traditional multi-head transformer encoder—pioneered by Vaswani et al.—is restructured. Instead of this complexity, the OGFormer employs the Single-Head Self-Attention (SSA) mechanism, streamlining attention calculations and significantly reducing computational load while still capturing crucial node relations.
To illustrate, let (Z^0 = X) denote the initial embedding for a node. Layer-by-layer updates using SSA are enabled through a concise formula that incorporates residual connections, which help prevent the network from losing important features as it deepens. The process is formalized as:
[
Z^l = \text{SSA}(Z^{l-1}, SE^l) + f(Z^{l-1}),
]
where (Z^l) represents the node embedding for layer (l), and (f) is a feedforward neural network layer.
Single-Head Self-Attention Mechanism
The SSA mechanism operates by utilizing a non-linear transformation that maps the query (Q) and key (K) into a shared latent space. In contrast to conventional transformer architectures where (Q) and (K) are projected into separate subspaces, OGFormer employs a shared transformation matrix. This design not only minimizes the number of parameters but also heightens computational efficiency.
The attention score matrix (R_{ij})—representing dependencies between nodes (v_i) and (v_j)—is calculated via:
[
R{ij} = \text{Norm}{j \in V}\left(\left(\hat{Q}_i \cdot \hat{Q}_j\right)^2\right),\quad \text{where } \hat{Q}_i = \frac{Q_i – \mu_i}{\sqrt{\sigma_i^2 + \epsilon}}.
]
Here, normalization ensures that the attention scores align with probability distributions, facilitating effective message passing between nodes.
Structural Encoding
While the SSA captures remote node dependencies efficiently, it is crucial to also integrate local structural information—especially for homophilous graphs, where nodes connected by edges often share attributes. Traditional graph neural networks (GNNs) compress local structural insights into low-dimensional vectors before amalgamating them with node features, often at the expense of losing critical relationships between nodes.
To improve upon this, the OGFormer introduces Structural Encoding (SE), which incorporates unbiased structural information (SE_{ij}) as a term in the attention score matrix:
[
\hat{R}{ij} = \text{Norm}{j \in V}(R{ij} + SE{ij}).
]
The structural encoding weighs the local connections to dynamically adjust for their influence on attention scores. This nuanced approach allows OGFormer to reflect genuine locality within graphs without compromising on efficiency.
Neighborhood Maximum Homogeneity Loss
In addition to enhancing graph representation learning through SSA and SE, OGFormer effectively addresses the need for homogeneity within neighborhoods of nodes. Introducing the Neighborhood Maximum Homogeneity Loss facilitates a balance between contextual information from the attention score matrix and the underlying distribution of node classes.
The relationship between attention scores and the target classes can be characterized using Kullback–Leibler divergence, helping to formulate a loss function that encourages class coherence within connected nodes. This is depicted as:
[
L{KL} = \sum{i,j \in V}\hat{R}{ij} D{KL}(Q_i || Q_j),
]
reinforcing the notion that similar nodes should have higher interaction weights.
To strengthen the emphasis on homogeneity within neighborhoods, a neighborhood homogeneity metric (h) is introduced:
[
Lh = \left|1 – h(\hat{R}{ij}, Y{train} || Y{pred})\right|_2,
]
ensuring that neighborhoods composed of similar classes reinforce their influence on the model more strongly than those with mixed classes.
By combining the influence of KL divergence and neighborhood homogeneity into a comprehensive loss function, OGFormer achieves a robust mechanism for learning in semi-supervised scenarios:
[
\mathscr{L}{NMH} = \sum{l=1}^L \lambda1^l L{KL}^l + \lambda_2^l L_h^l,
]
where (\lambda_1^l) and (\lambda_2^l) are hyperparameters adjusting the weight of respective loss components.
This in-depth exploration of the OGFormer model emphasizes its novel approach to attention score optimization, innovative structural encoding for local dependency capture, and enhanced loss functions that promote homogeneity in graph data contexts. The framework shines as a promising advancement in the evolving field of graph representation learning, paving the way for increasingly sophisticated applications and innovations.