Non-subsampled Shearlet Transform: An In-Depth Exploration

Introduction to Shearlet Transform

The Non-subsampled Shearlet Transform (NSST) emerges as a significant advancement within the composite framework of Wavelet Theory (WT), offering a robust multiscale analysis model. Wavelet Theory integrates techniques that focus on geometric selections, achieving high performance in various image processing tasks. The Shearlet Transform (ST) enables an optimally sparse representation of images, particularly those with distributed discontinuities. Its efficacy in Nonlinear Approximation (ONA) tasks has been well-documented, as demonstrated in studies involving medical image fusion.

Applications of Shearlet Transform

The ST’s strong directional sensitivity and localized time-frequency features have propelled its application across diverse image processing tasks including texture feature extraction, image denoising, and image fusion. This adaptability stems from the ST’s intrinsic ability to capture intricate structures within images, facilitating a nuanced analysis of visual data.

Discrete Shearlet Transform (DST)

Transforming from theory to application, the Discrete Shearlet Transform (DST) operates within the multiscale framework, leveraging the fundamental principles of wavelet theory.

1. Mathematical Framework: The DST is generated from a mother shearlet function represented mathematically. The transformation formula is expressed as:

   $${SH(\psi) = \left{ \psi_{j,l,k} = 2^{\frac{3j}{2}} \psi\left(G^{l}S^{j}x – k\right) : j \ge 0, -2^{j} \le l \le 2^{j}, k \in \mathbb{Z}^{2}\right}}$$

   Here, parameters include the scale index (j) for resolution adjustment, shear index (l) for directional selectivity, and translation index (k) for spatial positioning.

2. Constructing Matrices: The matrices (S) (anisotropic scaling) and (G) (shear matrix) play a critical role in refining frequency and establishing directional properties, respectively.

3. Frequency Domain Interaction: The application of the Fourier transform reveals insights into the frequency localization of the shearlet, assisting in edge detection and singularity representation effectively.

The Importance of Frequency Support

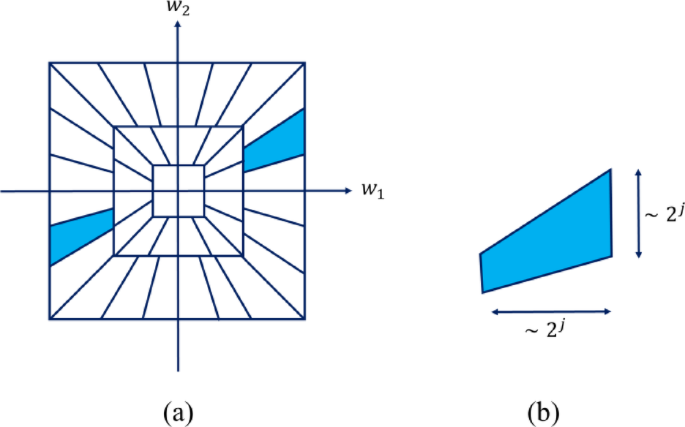
Analyzing the frequency support of shearlets emphasizes their directional localization abilities. The support regions, often trapezoidal in shape, are centered around slopes influenced by the shear parameter (l), allowing for a more refined identification of edges and curves compared to traditional transforms.

As the number of coefficients (N) increases, the asymptotic error associated with the Shearlet Transform approaches ({N}^{-2}(\text{Log}N)^{3}). This property enhances the precision of interferometric border selection and establishes a Parseval frame within the frequency domain, underscoring its robustness for various applications.

Challenges and Development of NSST

Despite the myriad advantages offered by the Shearlet Transform, inherent limitations arise from the subsampling operations commonly employed, which can lead to spectral aliasing and shift-variance. Consequently, the NSST was developed from the Non-Subsampled Contourlet Transform in order to mitigate these limitations.

1. Convolution-Based Filtering: By utilizing convolution-based directional filtering, the NSST ensures shift-invariance, thereby significantly diminishing the risk of pseudo-Gibbs phenomenon in image processing.

2. Decomposition Mechanism: The NSST decomposition consists of two key stages:
   • Multiscale Decomposition: Utilizes a Non-Subsampled Pyramid (NSP) for image decomposition into high-frequency components (HFC) and low-frequency components (LFC).
   • Directional Localization: Engages Non-subsampled Shearing Filter Banks (NSSFB) to facilitate effective directional analysis and filtering.

Advantages of NSST Over Other Transform Methods

The NSST holds distinct advantages compared to alternative multiscale transforms such as Discrete Wavelet Transform (DWT) and Non-Subsampled Contourlet Transform (NSCT). The shift-invariance characteristic of NSST preserves features while mitigating artifacts, notably at tissue boundaries in medical images. Also, its comparable directional selectivity comes with significantly reduced computational complexity—making the NSST more efficient.

Furthermore, the NSST achieves superior sparse representations of curvilinear structures, a critical capability when preserving anatomical fidelity in medical imaging environments.

The Impact of AlexNet and Neural Networks

In the context of evolving deep learning architectures, AlexNet stands out for its groundbreaking performance in the 2012 ImageNet Large Scale Visual Recognition Challenge (ILSVRC).

Architectural Features of AlexNet

• Layered Structure: Comprised of 8 learned layers—5 convolutional, 3 max-pooling, and connected fully connected layers—this architecture efficiently extracts features and reduces spatial dimensions.
• Kernel Utilization: The use of larger kernels in the initial layers emphasizes global data capture, particularly advantageous for low-frequency components.

Performance in Medical Image Fusion

AlexNet’s design proves beneficial for the Low-Frequency Selection Block (LFSB) fusion task. Relying on a balance of performance and computational efficiency, it facilitates multiple levels of feature extraction.

Innovative implementations enhance its effectiveness by enabling more contextual integration of features, thus yielding enhanced outputs in multimodal medical image analysis.

Concurrent De-noising and Enhancement Network (CDEN)

The CDEN brings two crucial functions into a single framework: de-noising and enhancing the image signals.

Structure of CDEN

1. De-noising Sub-Network (DNSN): This segment learns how to differentiate between clean and noisy components, feeding into a mapping function that aims to predict a clean signal based on noisy input.

2. EnhanceNet: Designed to generate probabilities indicating the class of original signals, it complements the de-noising capabilities by enhancing the feature extraction based on learned representations.

Implementation Strategies and Results

Multi-Layer Feature Generation

The process entails running images through AlexNet to derive multiple features across various layers, creating a feature-rich environment suitable for the adaptation of enhanced algorithms.

Adaptive Selection in Fusion

An Adaptive Selection Algorithm (ASA) operates in conjunction with the feature maps generated through AlexNet. This synergy ensures that the generated Weight Maps (WM) are contextually aware and optimal for merging structural and detail components of images, essential in medical diagnostics.

Pulse-Coupled Neural Networks (PCNN)

In the HFC fusion approach, the biologically inspired PCNN enhances image detail processing by simulating the neural feedback loop of the visual cortex. This mechanism effectively discriminates between significant features and noise, yielding a more reliable composite image.

By iterating over discrete time steps, the PCNN tailors its firing thresholds and integrates contextual feedback to optimize the fusion process, thus ensuring clarity and detail preservation within the final output.

Conclusion

The NSST and its implementation in the context of AlexNet and PCNN converge towards a robust framework for image processing, particularly within medical imaging. By addressing traditional limitations through innovative algorithms and neural networks, these approaches enhance diagnostic capabilities and improve visual clarity in multimodal applications.