Understanding the Primary Framework for Fake News Detection

In the quest to combat misinformation and enhance news accuracy, developing robust frameworks for fake news detection has become critical. This article delves into the architecture of our proposed model, highlighting its components, pre-processing techniques, word embedding strategies, and transfer learning adaptations.

Model Architecture

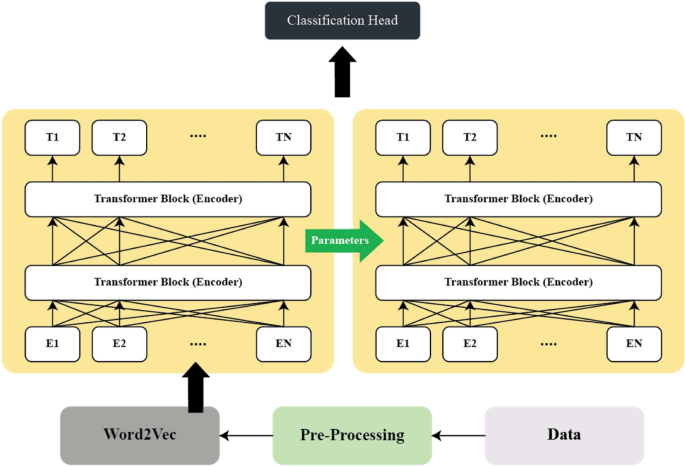
The architecture of our proposed model, as illustrated in Fig. 1, serves as a foundation for understanding how the various components interact to perform fake news detection. This comprehensive framework integrates pre-processing, embedding, and classification techniques to provide an effective solution against deceptive news articles.

Pre-processing

Successful data analysis begins with meticulous pre-processing. We adopted a suite of strategies designed to refine the textual data for better model performance.

1. Tokenization: The first step involves breaking down the text into individual words or tokens. This simplification makes further processing easier and more efficient.

2. Lower Casing: To unify the dataset, all tokens are converted to lower case, which ensures consistency during analysis. For example, ‘Data’ and ‘data’ are treated as the same word.

3. Stop-word Removal: Common words that do not contribute substantial meaning, such as “the”, “is”, and “and,” are eliminated to reduce noise.

4. Stemming and Lemmatization: These techniques convert terms to their base forms, helping the model recognize variations of the same word. For instance, both “running” and “ran” become “run”.

5. Part of Speech (POS) Tagging: Each word’s grammatical category is identified based on its usage in context. This tagging is pivotal for understanding how different parts of speech interact within deceptive and non-deceptive statements.

Mathematically, POS tagging can be expressed as:

$$\text{POS}(wi) = \arg \max {t_i} P(t_i \mid w_i)$$

Where (w_i) represents the words, and (t_i) their associated POS tags.

The importance of POS tagging lies in its ability to reveal syntactical patterns characteristic of fake news, such as exaggerated adjectives or specific grammatical constructions.

Word Embedding

Once pre-processing is complete, the next task involves transforming the cleaned text into a numerical format suitable for machine learning.

One-Hot Encoding

One approach is one-hot encoding, where each word is represented as a vector in a high-dimensional space. For every word, a binary vector indicates whether a specific character is present, assigning a "1" for presence and "0" for absence.

For example, with (B) total possible characters, the one-hot vector (v_{n,m}) can be illustrated as follows:

$$v_{n,m} = \begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \ B & -1 \end{bmatrix}$$

This transforms into a representative vector (V_{n,m}):

$$V_{n,m} = \sigma (WV \cdot v{n,m} + b_V)$$

Where (W_V) and (b_V) are optimized parameters during training.

Word2Vec

Word2Vec is a widely-used technique for generating word embeddings through neural networks. It utilizes two main architectures: Continuous Bag of Words (CBOW) and Skip-Gram.

• CBOW predicts a target word based on the context of surrounding words, optimizing distributed continuous contextual representations.

• Skip-Gram reverses this approach, using the target word to predict its surrounding context.

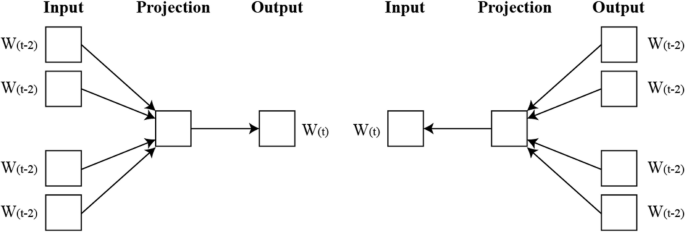
Fig. 2 illustrates the processes involved in both CBOW and Skip-Gram models.

Transfer Learning Using RoBERTa

The advent of RoBERTa represents a significant advancement in natural language processing. By leveraging pre-trained language models, we can significantly enhance performance on specific tasks, such as fake news detection.

The multi-stage transfer learning strategy employed demonstrates the effectiveness of pre-trained knowledge. Initially, the model is fine-tuned on a large, related corpus, enabling it to learn domain-specific features. Subsequently, a second fine-tuning phase focuses on smaller target datasets—like Politifact and GossipCop—to finely adjust the model.

Token and Positional Embeddings

RoBERTa begins its process by creating token embeddings for the input sequence. Each token (x_i) is converted into a high-dimensional vector using a learnable embedding matrix:

$$E(x_i) = W_e \cdot x_i$$

To account for the positions of tokens within the sequence, positional embeddings are added. Each positional embedding for a token at index (i) is computed as:

$$P(x_i) = W_p \cdot i$$

The final representation combines token and positional embeddings:

$$H_0(x_i) = E(x_i) + P(x_i)$$

Self-Attention Mechanism

RoBERTa incorporates a self-attention mechanism, allowing the model to evaluate the importance of each token relative to others in the input sequence. Each token generates three vectors: query (Q), key (K), and value (V):

$$Q= H_0(x_i) \cdot W_Q$$
$$K= H_0(x_i) \cdot W_K$$
$$V= H_0(x_i) \cdot W_V$$

The attention scores are computed as:

$$A_{ij} = \frac{Q_i \cdot K_j^\top }{\sqrt{d_k}}$$

This capability of distinguishing significant tokens enhances the contextual understanding of each word.

Multi-Head Attention and Layer Normalization

To capture varying contextual concepts within the text, multi-head attention processes several attention mechanisms in parallel. The outputs are concatenated and linearly transformed for optimal integration.

Layer normalization and residual connections are employed to stabilize the training process, facilitating effective convergence. The final representation after a layer (l) is:

$$H_l(xi) = \text{LayerNorm}\big(O{\text{multi-head}}(xi) + H{l-1}(x_i)\big)$$

Feed-Forward Neural Network

Each layer in RoBERTa includes a feed-forward neural network (FFN) operating independently on tokens. The output computation can be expressed as:

$$\text{FFN}(x) = \max(0, x W_1 + b_1) W_2 + b_2$$

This adds necessary non-linearity, bolstering the model’s capacity to process complex textual representations.

Pre-training Objective: Masked Language Modelling (MLM)

The pre-training phase involves masked language modeling (MLM), where random tokens are concealed, and the model learns to predict these missing elements based on context. The loss function for MLM is defined as:

$$L{\text{MLM}} = -\sum{m=1}^M \log P(xm \mid x{\setminus m})$$

This enables RoBERTa to develop a rich understanding of language structure and meaning.

Fine-Tuning

The fine-tuning of RoBERTa customizes the pre-trained model for specific tasks, updating its weights using labeled datasets. By adding task-specific output layers and optimizing the model via a loss function like cross-entropy, we maximize its accuracy in detecting fake news.

Incorporating early stopping and experimentation with layer freezing enhances the model’s generalization while mitigating overfitting—a critical consideration in low-resource scenarios.

By embracing this structured framework, we can significantly improve classification accuracy and overall robustness, ultimately leading to a more effective detection of fake news in today’s challenging media landscape.