Diamond Overview: Discovering Feature Interactions in Machine Learning
Introduction to Diamond
In the realm of machine learning (ML), accurately predicting responses from data can often involve understanding complex relationships among features. Consider a scenario where we have (n) independent observations, represented as matrices: (\mathbf{X} = {xi}{i=1}^{n} \in \mathbb{R}^{n \times p}) for features and (\mathbf{Y} = {yi}{i=1}^{n} \in \mathbb{R}^{n \times 1}) for responses. In many tasks, responses can be classified into categories (like disease status) or expressed numerically (such as body mass index). The challenge lies in effectively modeling these responses using an ML function (f: \mathbb{R}^p \mapsto \mathbb{R}), which reveals the dependence structure of (\mathbf{Y}) on (\mathbf{X}).
The Essence of Non-Additive Feature Interactions
A crucial focus of this study is on the non-additive feature interactions that significantly influence the predictions made by ML models. We designate (\mathcal{I} \subset {1, \ldots, p}) as a non-additive interaction if (f) cannot be decomposed into the sum of subfunctions, each omitting a corresponding interaction feature. For example, the interaction generated by multiplying two features, (x_i) and (x_j), illustrates non-additivity, whereas a logarithmic interaction can be decomposed additively, showcasing the complexity underlying feature relationships.
In practice, discovering these interactions requires careful attention. Our aim is to accurately identify critical interactions in (\mathcal{S}) while minimizing incorrect claims about interactions in the complement (\mathcal{S}^c).
The Diamond Approach: Feature Interaction Discovery
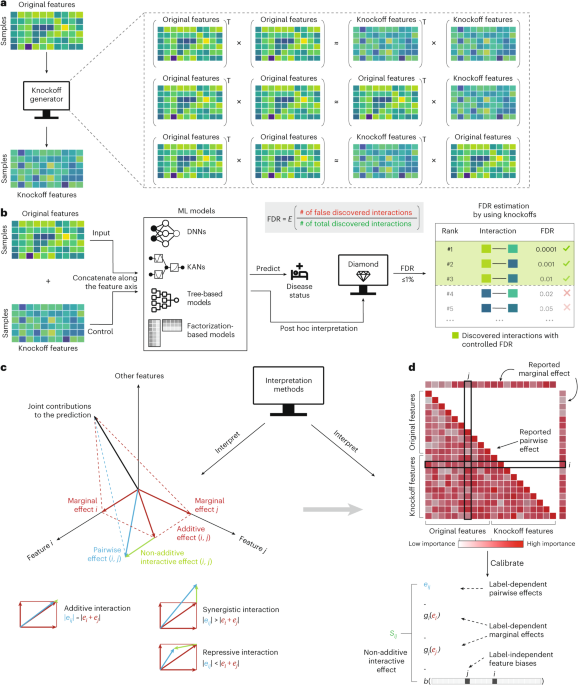
Diamond is engineered to unearth feature interactions while simultaneously controlling the false discovery rate (FDR). The FDR is defined as:
[
\text{FDR} = \mathbb{E}[\text{FDP}], \quad \text{with} \quad \text{FDP} = \frac{|\hat{S} \cap \mathcal{S}^c|}{|\hat{S}|},
]
where (\hat{S}) comprises the discovered interactions. Traditional methods, like the Benjamini–Hochberg procedure, generally control FDR through p-values calculated against a null hypothesis. However, generating reliable p-values for interactions, especially in complex ML models, poses substantial challenges.
To circumvent relying strictly on p-values while ensuring FDR control, Diamond employs the model-X knockoffs methodology. This technique generates knockoff features that mimic the original features but hold independence from the response, thus providing a baseline for assessing feature importance.
Training a Model with Knockoffs
Diamond constructs an augmented data matrix ((\mathbf{X}, \tilde{\mathbf{X}}) \in \mathbb{R}^{n \times 2p}) by concatenating the original features with their corresponding knockoffs. Once trained, Diamond evaluates feature interactions by interpreting model outputs and forming a ranked list of interactions. This process discerns non-additive interaction effects, filtering out both label-dependent marginal effects and label-independent feature biases to concentrate solely on significant interactions.
Evaluating Diamond’s Performance with Synthetic Data
Diamond’s utility shines through empirical trials on simulated datasets. These datasets present a mix of univariate functions and multivariate interactions with varying complexities. The objective is to detect pairwise interactions, constructing the ground truth from high-order functions.
Using a sample size of (n = 20,000) and (p = 30) features, our experiments revealed that Diamond reliably identifies important non-additive interactions while controlling the FDR. Specifically, models like multilayer perceptrons (MLP) and feature tokenizing transformers displayed exceptional performance due to their intricate capacity to decipher interaction complexities.
Distillation of Non-Additive Interactions
A pivotal discovery during these trials was that the non-additivity distillation process is indispensable for maintaining FDR control. Qualitative comparisons between interaction importance values before and after applying this distillation showcased significant discrepancies, further highlighting its necessity in filtering genuine interactions from spurious claims.
Real-World Application: Exploring Disease Progression
Transitioning from synthetic evaluations to practical applications, we assessed Diamond using a real-world dataset of 442 diabetes patients. The study aimed to uncover crucial interactions affecting disease progression through a diverse array of ML models—from MLPs to gradient boosting techniques.
Among the findings, Diamond proficiently identified notable interactions, such as between BMI and serum triglyceride levels, resonating with existing literature on diabetes risk. Furthermore, the model highlighted how these interactions collectively contribute to health outcomes, cementing Diamond’s relevance in clinical contexts.
Probing into Genetic Interactions: A Case with Drosophila
In another intriguing application, we utilized Diamond to analyze enhancer activity in Drosophila embryos, focusing on interactions among transcription factors and their contributions to genetic functions. The capability to identify known interactions through the learning process reinforced Diamond’s effectiveness in biological research, suggesting a fruitful pathway for future explorations into genetic interactions and enhancements.
Assessing Mortality Risk: Insights from National Studies
Evaluating mortality risk by analyzing a dataset from NHANES revealed additional dimensions of Diamond’s capabilities. Through interaction discoveries concerning mortality factors—such as the interplay between sedimentation rate and sex—Diamond aligned well with existing academic findings, demonstrating its potential in public health discussions.
As we delve deeper into advanced machine learning models and complex interactions among biological, health, and environmental factors, tools like Diamond pave the way for new insights and groundbreaking discoveries. Its methodology not only elucidates feature interactions but also controls significant rates of false discoveries, thereby enhancing the reliability of scientific findings across various disciplines.