Exploring Advanced Machine Learning Models for Time Series Analysis

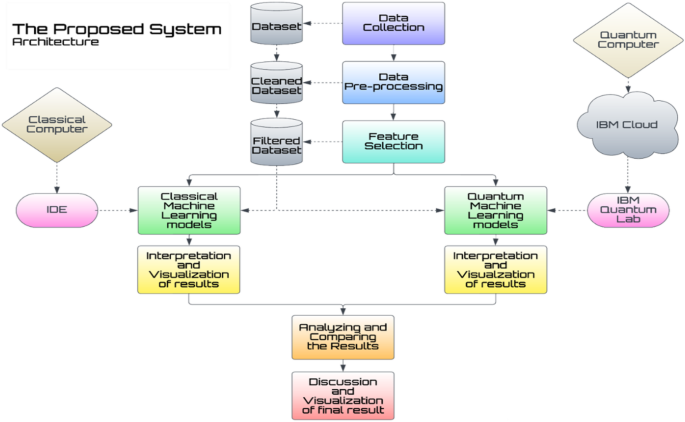
In recent years, the field of predictive modeling has witnessed significant advancements through the integration of classical machine learning, neural networks, and quantum machine learning algorithms. This article will delve into the various methodologies employed in our study, where we trained a dataset on three classical machine learning models, five neural network architectures, and three quantum machine learning algorithms, aiming for a comparative analysis.

Classical Machine Learning Algorithms

The study highlights classical machine learning approaches, particularly focusing on time series analysis and forecasting through three robust methodologies: Autoregressive Moving Average (ARMA), Autoregressive Integrated Moving Average (ARIMA), and Seasonal Autoregressive Integrated Moving Average (SARIMA). These methods have established a strong reputation in analytical tasks due to their robustness.

ARMA (Autoregressive Moving Average)

ARMA stands for Autoregressive Moving Average, a widely accepted statistical approach for time series forecasting. This model combines autoregressive (AR) and moving average (MA) aspects, leveraging past observations to predict future values.

• Autoregressive (AR) Model: Predicts the next value of a time series using prior data. The underlying assumption here is that the series’ current value is linearly dependent on its preceding values.

Mathematically, it can be defined as:
[
X{t} = c + \sum{i=1}^{p} \phi{i} X{t-i} + \sum{j=1}^{q} \theta{j} \epsilon_{t-j}
]

Where:

• (X_{t}): Value at time (t)
• (c): Constant term
• (\phi_{i}): Autoregressive coefficients
• (\theta_{j}): Moving average coefficients
• (\epsilon_{t}): White noise error term

ARIMA (Autoregressive Integrated Moving Average)

ARIMA enhances the ARMA model by incorporating an integrated (I) component, which differentiates the series to stabilize its mean. This helps when the data exhibits non-stationary behavior. Similar to ARMA, it employs AR components and integrates to account for the stationarity of the series.

The mathematical representation is:
[
\Delta^d X{t} = c + \sum{i=1}^{p} \phi{i} \Delta^d X{t-i} + \sum{j=1}^{q} \theta{j} \epsilon{t-j} + \epsilon{t}
]

SARIMA (Seasonal Autoregressive Integrated Moving Average)

SARIMA extends ARIMA to handle seasonal data effectively. It includes seasonal components alongside the regular AR, I, and MA components, resulting in an expansive capability for forecasting data with periodic patterns.

For our analysis, we employed SARIMAX in Python, tuning the ARMA method to (1, 0, 1), ARIMA to (2, 2, 2), and SARIMAX to a seasonal order of (15, 2, 5, 5).

Neural Networks

As we transition to deeper analytical methods, we explore various neural network architectures uniquely designed for time series analysis. The models include Long Short-Term Memory (LSTM) networks, Stacked LSTMs, CNN-LSTM hybrids, and ConvLSTM architectures.

Neural Networks with Swish Activation

The dataset was organized with the preceding five years as features and the sixth year as the output, resulting in an input size of five features. Our neural network model commenced with an input layer consisting of five neurons and concluded with a single-neuron output layer. Hidden layers, featuring 20 and 16 neurons respectively, utilized the Swish activation function, which is particularly effective for complex, temporal modeling tasks. A learning rate of 0.01 and 200 epochs of training were employed.

Vanilla LSTM

A Vanilla LSTM model was designed with 50 neurons in its LSTM layer, facilitating effective temporal dependency capture. The architecture began with five neurons, followed by an LSTM layer and a dense output layer.

Stacked LSTM

This advanced model incorporated two consecutive LSTM layers, each consisting of 50 neurons, followed by a dense output layer. Such a configuration enhances the model’s ability to extract intricate temporal patterns.

CNN-LSTM

Differing from traditional LSTM, this model included convolutional layers to process two-dimensional data. Reshaping the dataset into a 2×2 format allowed for the convolutional layer’s implementation, integrating feature extraction with temporal analysis effectively.

ConvLSTM

ConvLSTM operates on three-dimensional data structures, reshaping input data to a 1×2×2 format. It effectively captures spatiotemporal features, combining LSTM with convolutional capabilities for superior pattern recognition.

Quantum Machine Learning Algorithms

Exploring the cutting-edge realm of quantum computing, our study implements three key methodologies: Quantum Neural Networks (QNN), Variational Quantum Regression (VQR), and Quantum Support Vector Regression (QSVR). These approaches represent a substantial leap in predictive modeling capabilities.

QNN (Quantum Neural Networks)

QNNs represent a novel approach that fundamentally shifts how neural networks operate. Unlike traditional designs, they employ qubits to facilitate data processing through a network of qubit layers. With lossless dependencies, QNNs present a compelling option for advanced analytical tasks, leveraging IBM’s EstimatorQNN framework for their design.

VQR (Variational Quantum Regressor)

VQR specializes in regression tasks utilizing parameterized quantum circuits capable of adapting their structure dynamically. This powerful approach works through iterative parameter adjustments, impacting quantum circuits while minimizing output error.

QSVR (Quantum Support Vector Regressor)

Drawing parallels to classical Support Vector Regression but utilizing quantum kernels, QSVR enhances pattern detection capabilities, projecting data into high-dimensional spaces. Its functionality significantly improves predictive performance, particularly in structures where classical methods falter.

Quantum Advantage in High-Dimensional Data

Quantum machine learning algorithms exhibit unique advantages with high-dimensional datasets, minimizing the computational demand typically observed in traditional methods. Quantum algorithms exploit superposition and entanglement, demonstrating superior accuracy and processing efficiency. This is especially salient in QSVR, which utilizes quantum kernels to uncover complex relationships often overlooked by classical models.

Model Architecture Justification

The selection of model architectures was carefully guided by the need to address climate time series data characteristics while accommodating current quantum hardware constraints. For neural networks, the choice of LSTM with 50 neurons aligns with historical data dependencies analysis, and the Swish activation function has merited its use through superior performance metrics in temporal tasks. Quantum components were chosen with an eye toward optimizing expressibility amidst the limitations of NISQ devices, focusing on qubit counts that balance the complexity with computational feasibility. The COBYLA optimizer was particularly favored for its resilience to noise, ensuring robust performance throughout training.

The advancements in machine learning through these integrated methodologies — classical, neural, and quantum — not only pave the way for refined predictive capabilities but also herald a new era in data-driven decision-making across various applications, particularly in climate modeling.