Exploring Vehicle Fleet Dynamical Properties for Enhanced Traffic Management

In the ever-evolving landscape of transportation systems, understanding the dynamical properties of vehicle fleets is paramount. This article delves into the fascinating dynamics of a vehicle platoon, where multiple vehicles (denoted as (N)) travel in a single lane, following a lead vehicle. This arrangement allows for a plethora of behaviors and adaptations as vehicles dynamically respond to each other’s movements, creating a rich tapestry of interactions that can be quantified and analyzed.

Initial State and Response Dynamics

Imagine a scenario where a fleet of vehicles starts stationary. The lead vehicle accelerates, prompting a chain reaction that influences the speed of subsequent vehicles. Initially, the gap between the lead vehicle and the first following vehicle widens as the latter adjusts its speed. This chain of events continues, creating a ripple effect that propagates through the entire platoon until the last vehicle reacts. However, the dynamical nature of this system is further complicated by driver reaction times and the inherent delay in acceleration; oftentimes, trailing vehicles temporarily exceed the speed of the lead vehicle before correcting their speed.

The intricacies are captured by various mathematical car-following models, which simulate how drivers adjust their vehicles’ speed and distance based on their predecessors. One notable model is Krauss’s car-following model, characterized by a set of equations including:

[
v{\text{safe}}(t) = v{\text{l}}(t) + \frac{g{f}(t) – v{\text{l}}(t) \tau{r}}{\frac{v{f}(t) + v{\text{l}}(t)}{2 d{f}} + \tau_{r}} \tag{1}
]

[
v{\text{des}}(t) = \min[v{\max}, v{f}(t) + a{f} \tau{r}, v{\text{safe}}(t)] \tag{2}
]

[
v{f}(t+\tau{r}) = \max[0, v{\text{des}}(t) – \eta{f}] \tag{3}
]

These equations shed light on the interactions between vehicles, encapsulating the parameters that govern speed adjustments in response to the lead vehicle’s behavior.

Car-Following Dynamics and Network Effect

The complexity of vehicle dynamics is evident when examining speed fluctuations within the platoon. By treating the speed of each vehicle as an internal state of a dynamical system, we can derive the relationships that govern the speed changes across the fleet:

[
\begin{pmatrix}
v{2}(t+\tau{r}) \
\vdots \
v{N}(t+\tau{r})
\end{pmatrix} = \begin{pmatrix}
F{2}(v{1}, v{2}, a{2}, d{2}, g{2}, \eta{2}, t) \
\vdots \
F{N}(v{N-1}, v{N}, a{N}, d{N}, g{N}, \eta{N}, t)
\end{pmatrix} = \mathcal{F}(v_{1}, v, a, d, g, \eta, t) \tag{5}
]

This formulation emphasizes how the interconnected nature of the fleet amplifies the overall dynamics. Each vehicle’s speed is influenced by its predecessor, leading to complex nonlinear behaviors that can be harnessed for computational purposes.

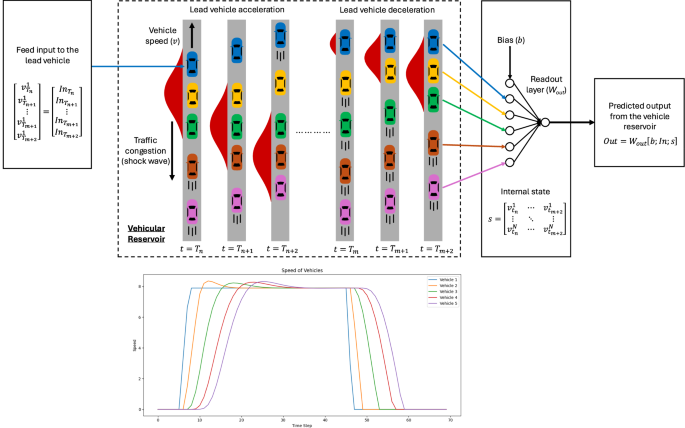
Leveraging Nonlinearity: Vehicular Reservoir Computing

The established nonlinear properties of the vehicle platoon set the stage for an innovative computing paradigm—vehicular reservoir computing (VRC). Shock waves emerge when a lead vehicle suddenly decelerates, creating stop-and-go phenomena known as traffic shock waves. Such nonlinear dynamics can serve as computational resources when harnessed appropriately.

In VRC, the state of the system (i.e., the collective speeds of vehicles) provides a reservoir of dynamical features that can help predict and adapt to various tasks. Here’s how it works:

1. Input Transformation: The speed of the lead vehicle is manipulated as input for the system, denoted as (v_{1}). The remaining vehicles adjust their speeds accordingly based on Krauss’s model.

2. State Representation: The internal state of the reservoir is defined as (s := [v{1}; \ldots; v{N}]), allowing the model to encapsulate the conditions affecting each vehicle.

3. Output Generation: Outputs are generated based on a linear combination of the internal state and input signals, formulated as:

[
O := W_{o}[b; In; s] \tag{Output Equation}
]

The simplicity of linear regression for training the output weight matrix ((W_{o})), as shown below, stands in contrast to complex deep learning frameworks, offering a unique advantage.

[
W{o} = T{o} [b; In; s]^{T}([b; In; s][b; In; s]^{T})^{-1} \tag{7}
]

Fully Utilizing Human Driving Behavior for Learning Capacity

Initial experiments involving simulations reveal intriguing insights about how various driving policies impact learning outcomes. When employing real-world traffic simulation tools like SUMO, the relationship between heterogeneous driving behaviors and learning capacity becomes compelling. The chaotic driving styles, inherent variances among drivers, and differing acceleration/deceleration patterns elevate the nonlinear nature of the reservoir, enhancing its learning capacity.

Congestion Level and Learning Performance

A significant aspect of VRC is how performance correlates with the congestion levels present in the vehicle platoon. The interplay between diverse driving behaviors not only creates rich dynamics but also serves as an effective computational asset. Experimental data indicates that as congestion levels increase, learning capacity improves—a fascinating paradox to the traditional view of congestion as a mere traffic hindrance.

System Sensitivity to Latency and Stochastic Noise

Venturing into practical applications, the sensitivity of the VRC system to latency and noise emerges as critical factors for real-world usability. Introducing delays, even mild ones, can significantly lower prediction accuracy, emphasizing the importance of minimizing latency in vehicle systems. Similarly, real-world driving behavior presents inherent stochastic elements, further complicating the system dynamics but also providing robust performance under variances similar to actual driving scenarios.

By analyzing how fluctuations affect vehicle interactions, a nuanced understanding of how to leverage non-linear dynamics for enhanced computational tasks becomes tangible. This intricate balance between chaos and order fosters both robustness and adaptability in vehicular reservoir computing.

The Road Ahead

As we move toward automating and integrating transportation systems, appreciating the dynamical properties of vehicle fleets will become increasingly important. Continued exploration into how vehicular dynamics can serve as both a metaphorical engine and a literal reservoir for computation opens the door for an array of innovations in machine learning and traffic management solutions, promising safer and more efficient transportation systems in the near future. Understanding these complex interactions will ultimately shape the future of transportation, driving us toward smarter roads and more connected vehicles.