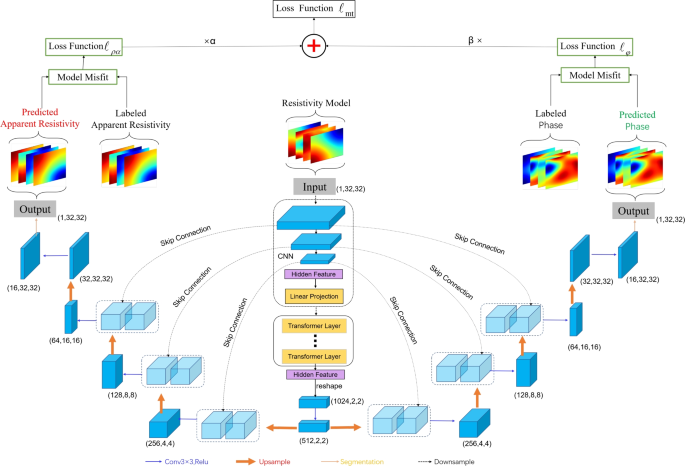
Dataset Preparation for Multitask Network Learning in Geoelectrics

Introduction

In the fast-evolving field of geophysical modeling, particularly when it comes to magnetotelluric studies, the importance of quality dataset preparation cannot be overstated. Prior to engaging in multitask network learning, practitioners face the crucial task of generating synthetic datasets tailored for effective neural network modeling. This process plays a vital role in closely mimicking actual subsurface resistivity structures, thus enhancing model reliability and applicability.

Characteristics of Resistivity Structures

One of the primary attributes of subsurface resistivity models lies in the gradual variation of resistivity values. Unlike simplistic anomaly bodies or basic high-low resistivity models, modern approaches utilize cubic spline interpolation to generate intricate resistivity model sets. This technique creates a spectrum of resistivity values, facilitating a more realistic representation of subsurface conditions. As a result, the training datasets developed from these models significantly mirror real-world measurement environments, increasing their practical utility.

Designing the Synthetic Model

The synthetic model designed for this study spans a substantial area of 5 km by 3 km. Within this framework, essential parameters are set: (H) (the number of frequencies) and (L) (the number of observation points) are both set to 32, with frequencies ranging from 0.05 to 320 Hz. Resistivity values are varied within an extensive range of 0.1 to 100,000 (\Omega \cdot m). By merely adjusting the model size and parameters (H) and (L), new datasets tailored for different tasks can be crafted effortlessly. Ultimately, 20,000 sample data points were generated, with 80% allocated for training, 10% for validation, and the remaining 10% reserved for testing purposes.

Importance of Normalization in Neural Networks

Normalization serves as a cornerstone in neural network training, greatly influencing the stability and effectiveness of the learning process. By maintaining consistent input distributions, particularly within deep neural networks, normalization addresses potential issues like gradient vanishing and explosion. Furthermore, it enhances the stability of weight adjustments, curbing sensitivity to learning rates and initial weight selections.

When it comes to processing geoelectric model data, the first step involves applying a base-10 logarithm to the resistivity data. For impedance phase data, the values remain unchanged due to their smaller range. Subsequently, maximum and minimum values are derived, mapping actual values to a normalized range of [0, 1]. The process is outlined mathematically as follows:

Normalization Equations

For general resistivity data, the following equation is applied:

[
Y = \frac{{\log_{10} X – \text{min}}}{{\max – \text{min}}} \quad (7)
]

Meanwhile, for the impedance phase, the equation modifies slightly:

[
Y = \frac{{X – \text{min}}}{{\max – \text{min}}} \quad (8)
]

Inverse Mapping for Neural Network Predictions

When predicting forward responses using neural networks, inverse mapping becomes essential. For apparent resistivity, the inverse mapping formula is:

[
x’ = 10^{(\max – \min) \cdot y’ + \min} \quad (9)
]

For impedance phase predictions, the inversion follows this equation:

[
x’ = (\max – \min) \cdot y’ + \min \quad (10)
]

In these equations, (x’) represents the actual predicted values from the neural network, while (y’) signifies the neural network’s output.

Training Parameters and Efficiency

During the model training phase, a sigmoid activation function is employed alongside Mean Squared Error (MSE) loss for optimization. The Adam optimizer is selected to minimize training time while enhancing the performance of the T-Unet model. Key training parameters include a learning rate of 0.001, batch size of 10, and the completion of 100 training epochs.

The loss function curve observed during training visually demonstrates the model’s progression, indicating areas of improvement as the network honed its predictive capabilities.

Mean Squared Error Calculation

The MSE is computed using the formula:

[
\text{MSE} = \frac{{\sum\limits{i=1}^{H} \sum\limits{j=1}^{L} |T{i,j} – P{i,j}|^2}}{{H \times L}} \quad (11)
]

Where (H) and (L) represent the dimensions of the input data, while (T) and (P) represent the true and predicted values, respectively.

Conclusion

This exploration into dataset preparation underscores its pivotal role in the development of neural network models for geoelectric applications. By outlining the methods applied—from resistivity structure modeling, normalization processes, and training methodologies—this article demonstrates the systematic approach necessary for deploying robust and effective predictive models in practical environments. As the landscape of machine learning in geophysics evolves, so too does the need for precise, reliable datasets that can withstand the complexities of real-world applications.