Application of DR-PINNs to the Poisson Equation
The Poisson equation, a cornerstone in mathematical physics, plays a significant role in modeling various phenomena such as electrostatics, heat conduction, and fluid dynamics. This equation describes the steady-state distributions influenced by spatially varying sources. A common formulation of the two-dimensional Poisson equation is:
[
\frac{\partial }{\partial x} \left( c(x,y) \frac{\partial u}{\partial x} \right) + \frac{\partial }{\partial y} \left( c(x,y) \frac{\partial u}{\partial y} \right) = 1, \quad x \in [0,1], y \in [0,1]
]
with the boundary conditions set as:
[
u(0,y) = u(1,y) = u(x,0) = u(x,1) = 0
]
This setup is particularly intriguing as it allows for the exploration of piecewise continuous coefficients, introducing discontinuities in material properties. Specifically, the diffusion coefficient (c) can be defined as follows:
[
c = \begin{cases}
1, & 4x – 2y \le 1 \
2, & 4x – 2y > 1
\end{cases}
]
Problem Representation
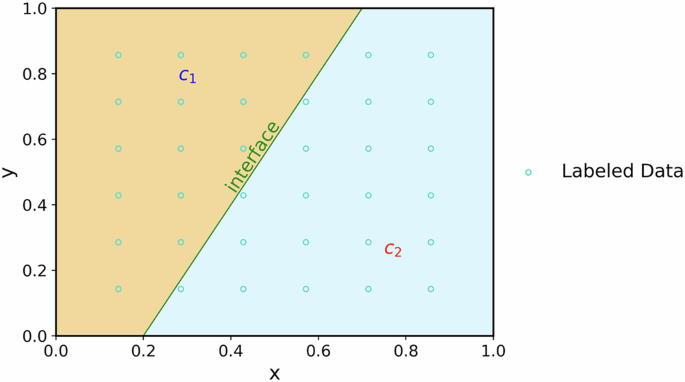
In the unit-square domain, illustrated effectively in Fig. 1, we explore how this setup can be leveraged using DR-PINNs (Deep Reinforcement Physics-Informed Neural Networks). The domain is segmented into two sub-regions with different diffusion coefficients, providing a vivid representation of material discontinuities.
Training Process and Architecture
To facilitate the training process, a uniformly distributed grid of labeled solution points is established, notably a 6 × 6 grid. Alongside, 2000 randomly sampled training points are utilized to train a fully connected neural network. The architecture consists of three hidden layers with 50 neurons each, specifically designed to output the required physical quantities, based on inputs of (x) and (y). A subsidiary network with three hidden layers and 20 neurons is tasked with predicting values at the interface, using (4x – 2y – 0.5) as input.
The training procedure utilizes a two-phase approach: an initial training phase with a learning rate of (10^{-3}) for 20,000 epochs, followed by an additional 30,000 epochs at a reduced rate of (10^{-4}). Supplementary Fig. 1 highlights the iterative training results, demonstrating a rapid decline in the loss function and quick convergence of the unknown parameters. By the time the learning rate diminishes, the parameter (c) converges accurately to its true value.
Performance of DR-PINN
The performance of DR-PINNs in capturing the distinct features of the target functions using a straightforward architecture is commendable. The approach remarkably minimizes the necessity for extensive hyperparameter tuning, facilitating an efficient and accurate modeling of the underlying physics.
Application to Beam Problems
Euler-Bernoulli Beam Under Static Loads
The Euler-Bernoulli beam equation serves as an exemplary high-order problem, showcasing the capabilities of DR-PINNs when applied to traditional engineering scenarios. The equation governing the beam under static loads is compounded by displacement discontinuities in scenarios with varying cross-sections. The governing equation is stated as:
[
-\frac{d^2}{dx^2} \left( EI(x) \frac{d^2 w(x)}{dx^2} \right) + q(x) = 0
]
Key parameters include (w(x)) as the transverse displacement and (q(x)) representing the transverse load. Typical engineering scenarios depict shear forces that demonstrate discontinuities, as they do not satisfy the (C^1) continuity condition.
Load Cases
The analysis spans multiple load cases, characterized by the varying lengths of the concentrated load’s influence, defined through (q(x)). The variability in these load scenarios accentuates the complexity faced during parameter estimation.
Network Configurations for Parameter Identification
In the dynamic landscape of this problem, networks (\hat{w}), (\hat{\varphi}), (\hat{M}), and (\hat{V}) model the physical interactions, while dedicated networks emphasize the relationship between bending moments, slopes, and curvatures. The complexity is further exacerbated by the inherent coupling between these parameters.
DR-PINNs strategically tackle the challenges posed by discontinuities. By partitioning the beam domain and establishing loss functions that directly correlate to the flexural stiffness identification, DR-PINNs can effectively manage and reduce computational burdens while retaining accuracy and efficiency.
Comparative Analysis with Traditional PINNs
To illustrate the efficacy of DR-PINNs, traditional PINNs and XPINNs (Extended Physics-Informed Neural Networks) were employed as benchmarks against which DR-PINNs were evaluated. Figures showcasing the performance metrics reveal that DR-PINNs maintain a superior capacity for handling loads with steep discontinuities, evidenced through consistent low loss values across varying scenarios.
Application to Dynamic Loads
Transitioning into dynamic scenarios with the beam under dynamic loads, the governing equation is refined to incorporate inertia represented by density, (\rho), giving rise to the equation:
[
\rho A(x) \frac{\partial^2 w(x,t)}{\partial t^2} + \frac{\partial^2}{\partial x^2} \left( EI(x) \frac{\partial^2 w(x,t)}{\partial x^2} \right) = f(x,t)
]
where (f(x,t)) encapsulates the dynamic load profile. It is crucial to note the significant computational challenges presented by dynamic loading conditions and the complexity introduced by the spatially distributed unknown parameters.
Training Mechanisms and Performance Metrics
Training under dynamic loading further emphasizes differences in performance among DR-PINNs, PINNs-Gaus (Gaussian approximated loads), and PINNs-Delt (Dirac-delta function loads). The loss function curves portray a distinct advantage for DR-PINNs, achieving significant reductions in final loss values — by more than two orders of magnitude compared to its counterparts.
Application to Thin Plate Problems
The study extends into thin plate structures, which are prevalent across diverse engineering fields, presenting unique challenges due to potential material damages and parameter discontinuities identified through high-order differential equations. The governing equation for thin plates introduces complexities with higher-dimensionality responses and the coupling of directional reactions.
The parameters defining the elastic modulus of the plates provide a foundation for the application of DR-PINNs, addressing sudden changes effectively. The established training regime, with randomized sampling strategies and iterative corrections, demonstrates robustness in capturing the nuances of physical distribution in loaded plates.
Conclusion of Computational Efficiency
As demonstrated across derivations and applications, DR-PINNs reveal significant enhancements in computational efficiency compared to traditional methods, especially as problem complexity escalates. The structured interplay between physics and labeled data ensures accurate parameter identification in scenarios previously deemed challenging.
Playing a transformative role in engineering simulations, DR-PINNs are poised to reshape conventional methodologies, fostering unprecedented accuracy and efficiency in solving complex partial differential equations across varied disciplines.