Statistical Analysis of Symbolic and CFD-Inspired Datasets for Proppant Settling Rate

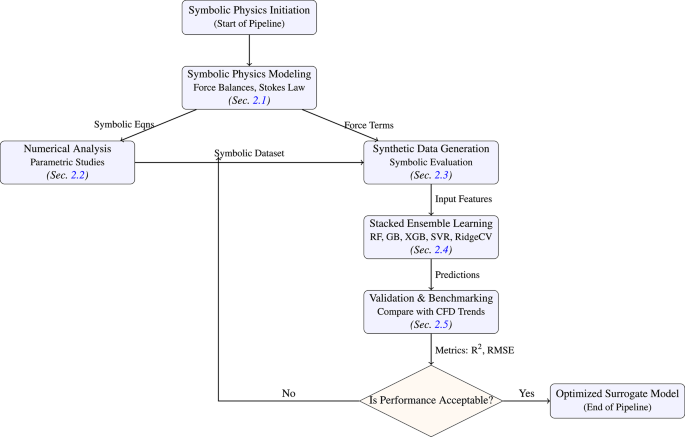
A comprehensive statistical analysis has been undertaken to evaluate and contrast two datasets crucial for modeling proppant settling rates (PSR): the symbolic dataset, generated using closed-form physical equations, and the CFD-inspired dataset, derived from a literature-informed sampling of multiphysics variables. This analysis aims to elucidate the structural and statistical foundations of both datasets, forming a foundation for subsequent model development and generalization strategies.

Distributions and Characteristics of Datasets

Initial analyses, as indicated in Tables 1 and 2 and visualized in radar plots (Fig. 2), reveal substantial differences in the data distributions of the two datasets. The symbolic dataset is constructed under simplified assumptions based on Stokes’ law and relevant formulations. It features constrained variability, characterized by constant values for gravity and fluid density, indicating a theoretical isolation of variables. While proppant density, diameter, and viscosity span moderate ranges akin to laboratory-scale investigations, the radar plot highlights pronounced peaks for viscosity and particle size, underscoring their significance in classical PSR equations.

Conversely, the CFD-inspired dataset exhibits a broader and more balanced statistical profile. By incorporating variables such as inlet slurry velocity, outlet pressure, elastic modulus, and fracture geometry, this dataset captures the complexities of subsurface dynamics. The higher standard deviations across various features point to the natural operational heterogeneity and multifactorial coupling typical of field-scale simulations. The radar plot for this dataset presents a flatter distribution pattern, indicating equitable representation across features. This contrast brings to light a critical tradeoff: the symbolic dataset provides clarity and interpretability, making it suitable for theoretical validation. In contrast, the CFD dataset fosters learning within high-dimensional, realistic regimes, paving the way for hybrid modeling that bridges idealized physics and data-driven generalization in hydraulic fracturing contexts.

Validation through Numerical ODE Simulation

To validate the symbolic force-balance formulation, the governing ordinary differential equation (ODE) for the vertical motion of a proppant particle suspended in a viscous fluid was numerically solved. The model incorporates various forces acting on the particle, such as gravitational, buoyant, viscous drag, and elastic forces induced by micro-strain. The transient velocity profile generated (Fig. 3) illustrates a rapid acceleration phase followed by convergence to a steady-state terminal velocity, reflecting drag-limited settling dynamics.

The ODE represented by the equation is given as:
$$
m_p \frac{dv}{dt} = V_p (\rho_p – \rho_f) g – \frac{1}{2} C_d \rhof A v^2 – k\epsilon \epsilon
$$
where (Cd) is the drag coefficient, (k\epsilon) represents the strain stiffness constant, and (\epsilon) signifies imposed elastic strain. Analyzing the numerically modeled terminal velocity reveals consistency with the analytical Stokes prediction, thus validating the symbolic formulation in low-to-moderate Reynolds regimes.

However, the observed terminal velocity marginally exceeds the textbook Stokes prediction due to several factors, including the influence of drag corrections and the finite initial velocities of the fluid, leading to rapid inertial responses. The analytical framework thus offers a computationally efficient alternative to comprehensive CFD–DEM simulations, with potential for providing benchmark datasets for training surrogate models like Physics-Informed Neural Networks (PINNs).

Parametric Sensitivity Analysis

To study the effects of geometric and mechanical parameters on proppant settling, parametric analyses were conducted considering variations in particle diameter and formation strain. Notably, larger particle diameters resulted in significantly faster terminal settling rates, affirming Stokes’ law predictions, which dictate a quadratic dependence on diameter. Conversely, increased formation strain led to decreased settling velocities, owing to the opposing elastic resistance incurred.

Figure 4 encapsulates these results, demonstrating a clear relationship between particle diameter and settling velocity, with an increase from 0.5 mm to 1.0 mm culminating in enhanced terminal settling speeds. In contrast, applying formation strains in the range of (\epsilon = 0.01) to (0.10) introduced a damping effect on particle descent, illustrating the vital role of particle-fluid interaction physics in controlling settling behaviors, particularly in unconventional reservoirs where local flow fields can be significantly affected by formation dilation or compaction.

Influence of Pressure Drop on Proppant Transport

To extend symbolic model applicability further, the effect of pressure gradients on proppant mobility was examined. Simulations were conducted with pressure gradients of 0.1, 0.5, and 1.0 bar/m to assess their implications on settling dynamics. The interplay of pressure-induced flow fields opposing gravity was integrated into the symbolic formulation using a Bernoulli-inspired term modulated by fracture deformation.

At lower gradients, drag was negligible, enabling efficient particle settling. However, at higher gradients, as shown in Fig. 5a, the interaction between pressure-driven flow and drag resistance significantly reduced settling velocity. This finding underlines the operational trade-off between fracture propagation and proppant transport efficiency.

Additionally, evaluating the influence of proppant density on settling behavior reinforced expected theoretical outcomes. Simulations for densities ranging from 2500 to 3500 kg/m³ (Fig. 5b) exhibited deeper settling trajectories and faster descent rates for denser particles, corroborating the linear relationship between density and net gravitational force.

Combined Effects of Diameter and Density

A symbolic surface model was developed to jointly assess the interplay between proppant diameter and density on settling velocity. The resulting response surface confirms a monotonic increase in velocity with both parameters, consistent with fluid mechanics principles. Within the Stokes flow regime, rising diameter leads to increased gravitational force, while higher density enhances net downward force, thereby improving settling rates.

Moreover, symbolic expressions analyzing pressure drops as a function of variable parameters revealed that pressure losses increase quadratically with diameter and density, decrease with fracture height, and rise with inlet velocity (Fig. 7a & 7b). This rigorous parametric analysis validates the predictive structure of the symbolic model, empowering rapid exploration of operational trade-offs in fluid dynamics.

Settling Rate and Drag Force Analysis

The settling characteristics of proppants are fundamentally influenced by the competing forces of gravity, buoyancy, and drag. A symbolic parametric analysis reveals that both proppant density and diameter positively correlate with settling rate, aligning with theoretical expectations derived from Stokes’ dynamics (Fig. 8a). However, influencer behavior illustrated in (Fig. 8b), shows that drag force increases steadily with diameter, reaffirming its strong dependence on surface area and velocity.

Predictive Performance of Models

The statistical evaluation of machine learning models built upon both symbolic and CFD-inspired datasets indicated impressive predictive performance (Fig. 9). The symbolic model, grounded in physics principles, achieved noteworthy generalization metrics contrasted with slightly higher scores from the CFD-based model. Furthermore, a combined stacked ensemble model yielded the highest performance, illustrating the benefits of integrating physics-based and empirical representations.

Interpretability and Feature Importance Analysis

Feature importance and partial dependence analyses shed light on model interpretability, revealing that inlet slurry velocity is the most significant determinant across model configurations. Secondary influences arose from fluid viscosity and proppant density, while proppant diameter demonstrated relatively minor effects. These insights reinforce the importance of operationally relevant factors in hydraulic fracturing processes.

Uncertainty Quantification in Predictions

To assess the reliability of model predictions, uncertainty quantification was performed using ensemble variance methods. The analysis indicates that uncertainty tends to escalate with higher predicted PSR values, echoing expected behaviors when extrapolating beyond core training distributions. Such uncertainty estimates can be instrumental for risk management in proppant placement optimization.

Correlation Assessment

Finally, an evaluation of the Pearson correlation matrix across input features highlighted a low correlation among variables, minimizing multicollinearity, and supporting robust model training.

Real-world Implications

In practice, the hybrid symbolic-ML framework emerges as a computationally efficient alternative to traditional CFD simulations for predicting proppant settling dynamics. However, future work should aim to validate these synthetic datasets against empirical data, address the limitations of the model’s assumptions, and potentially adopt explainable AI methodologies to enhance interpretability.

This structured analysis presents a significant step toward integrating empirical validation and multi-physics generalization, enriching our understanding of proppant transport models in hydraulic fracturing contexts.