Understanding LoRA and Fine-tuning in Large Language Models
In recent years, advancements in natural language processing (NLP) have led to significant strides in developing large language models (LLMs). One of the most captivating developments is the advent of Low-Rank Adaptation (LoRA). This technique is poised to change how we fine-tune LLMs, particularly in specialized tasks like coding and math problem-solving. Here, we’ll dive deep into the elements that define LoRA and explore the surrounding landscape of fine-tuning LLMs.
Abstract and Introduction
At its core, LoRA addresses the challenges posed by full fine-tuning of large-scale models, where complete parameter updates can often lead to unnecessary computational costs and even hinder model performance in certain contexts. The unique positioning of LoRA lies in its ability to maintain efficiency without sacrificing effectiveness by only updating a low-rank subset of parameters during training.
Background
To fully grasp LoRA’s impact, it’s essential to examine the intricacies of traditional fine-tuning and the challenges it presents. Conventional methods involve updating all model parameters, which can be resource-intensive and lead to overfitting, especially in tasks requiring high adaptability. LoRA simplifies this by strategically adjusting a portion of parameters while keeping the majority intact, thus reducing the risk of degrading the model’s baseline capabilities.
Experimental Setup
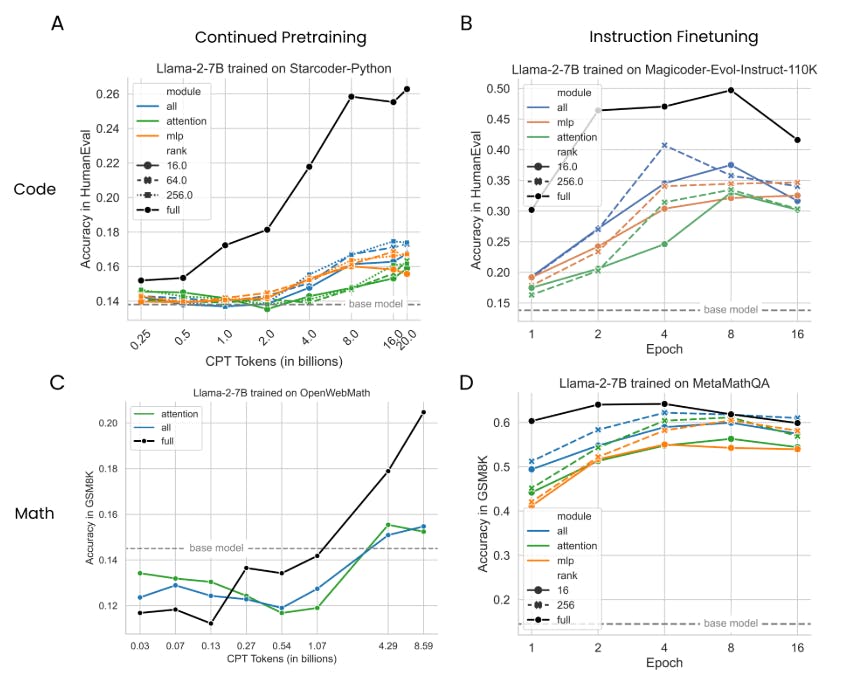
Datasets for Continued Pretraining (CPT) and Instruction Fine-tuning (IFT)
When implementing LoRA, careful consideration must be given to the choice of datasets. For effective performance in specialized domains, it’s crucial to have datasets that align well with the desired tasks. The general data used for continued pretraining and fine-tuning should encompass representative samples to enhance the model’s learning capacity.
Measuring Learning with Coding and Math Benchmarks
In exploring the efficacy of LoRA, benchmarks in coding and mathematics serve as critical evaluation tools. These benchmarks not only provide a litmus test for performance but also give previously unseen insights into how well a model can adapt to new challenges and scenarios, highlighting strengths and potential areas for improvement in the context of LoRA.
Forgetting Metrics
Another essential parameter in the evaluation of LoRA involves measuring forgetting metrics. This aspect investigates how models retain information from original training sets when exposed to new tasks. The focus here is on ensuring that essential knowledge remains even after additional training.
Results
LoRA Underperforms Full Fine-tuning in Programming and Math Tasks
While LoRA offers significant benefits, research indicates that it may not always surpass full fine-tuning techniques in certain high-demand tasks. In programming and complex mathematical contexts, deeper, more extensive training often yields stronger results. This finding compels practitioners to consider the trade-offs between efficiency and comprehensive skill development.
LoRA Forgets Less than Full Fine-tuning
One clear advantage observed in studies is that LoRA tends to retain more of the initial training knowledge than full fine-tuning methods. This observation suggests that while fine-tuning broadens skill application, LoRA’s refined approach allows the model to "remember" its foundational training better.
The Learning-Forgetting Tradeoff
Understanding the dynamics between learning and forgetting is pivotal when deploying models in real-world scenarios. LoRA establishes itself as a viable option for those looking for a balance between expanding capabilities and preserving the integrity of learned tasks.
LoRA’s Regularization Properties
A fascinating attribute of LoRA is its inherent regularization strength. By adapting the model with fewer parameters, it implicitly controls the potential for overfitting. This aspect is essential for practical applications where data might be limited or highly specialized.
Full Fine-tuning on Code and Math Does Not Learn Low-Rank Perturbations
Interestingly, research shows that traditional full fine-tuning methods do not effectively capture low-rank solutions, which are fundamental to the principles behind LoRA. Thus, while full fine-tuning offers a broader brushstroke approach, it can miss out on nuances that are critical for specialized tasks.
Practical Takeaways for Optimally Configuring LoRA
To harness the full capabilities of LoRA, practitioners should adopt best practices in configuration. This includes thoughtful consideration of hyperparameters, which can significantly influence performance outcomes. Fine-tuning LoRA requires an acute awareness of the balance between model capability and computational efficiency.
Related Work
The landscape surrounding language model fine-tuning is vast and includes numerous studies and methodologies. Research efforts aimed at refining and analyzing processes coexist alongside practical applications in diverse fields from academia to software development. Examples include LLMs adapted for specific programming languages or the investigation into various benchmarks for evaluating model performance.
Discussion
Does the Difference Between LoRA and Full Fine-tuning Decrease with Model Size?
The relationship between model size and the effectiveness of various fine-tuning methods remains an open question in the field. Initial findings suggest that larger models may exhibit diminishing differences between fine-tuning approaches. However, this area requires further exploration to uncover the intricacies of scaling properties.
Limitations of the Spectral Analysis
While the spectral analysis showcases the dimensionality of solutions obtained through full fine-tuning, it does not completely dismiss the potential for low-rank adaptations. The complexity of the models indicates that the rank required to construct a weight matrix can vary depending on the downstream task requirements.
Why Does LoRA Perform Well on Math and Not Code?
The varied performance of LoRA in math versus coding tasks raises pertinent questions. One possibility is the difference in domain complexity between the two fields. Mathematical datasets often present a more homogenous structure, potentially leading to enhanced learning and retention when models are fine-tuned. In contrast, coding tasks can introduce complexities that challenge even the most robust models.
By understanding these intricate dynamics, researchers and practitioners can better navigate the evolving landscape of large language model training and fine-tuning, leveraging techniques like LoRA for more efficient and effective outcomes.