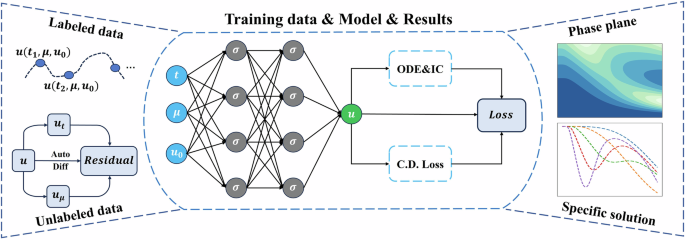
Numerical Experiments on Ordinary Differential Equations and the Application of cd-PINN
In this section, we delve into detailed numerical experiments involving a variety of ordinary differential equations (ODEs), including well-known models such as the Logistic growth model, the Lotka-Volterra model, damped harmonic oscillators, a multiscale model for p53 activation, the Lorenz system, and the 2D wave equation. These experiments prominently showcase the impressive generalization abilities of our continuous dependently informed Physics-Informed Neural Network (cd-PINN). Following these explorations, we summarize and discuss crucial issues linked to the performance and setup of cd-PINN.
The Logistic Model
We begin with the Logistic growth model, a cornerstone in population dynamics formulated by Pierre Verhulst. This classical equation describes population growth regulated by carrying capacity due to resource limitations and is given by:
[
\frac{du}{dt} = ru\left(1 – \frac{u}{u_{\text{max}}}\right)
]
Where ( u(t) ) represents the population size, ( u_{\text{max}} ) is the carrying capacity, and ( r > 0 ) denotes the growth rate. By applying separation of variables, we derive its general solution:
[
u^*(t) = \frac{u(t)}{u{\text{max}}} = \frac{1}{1 + e^{-rt}(u{\text{max}}/u_0 – 1)}
]
where ( u_0 ) is the initial population size. We find that the solution to the logistic equation is continually differentiable relative to both ( r ) and ( u0 ). Notably, the logistic equation has two fixed points: ( u = 0 ) (unstable) and ( u = u{\text{max}} ) (stable), with the latter being the attraction basin for positive disturbances.
For our experiments, we generated 20 real data points at ( t \in [0.0, 0.5] ) using ( u_0^ = 0.3 ) and ( r = 1.0 ). Additionally, we explored a total of 1,600 sets of ((u_0^, r)) pairs, resulting in 32,000 data points for testing. A fully connected neural network with six hidden layers and 128 neurons in each layer was trained utilizing the Adam optimizer for the initial 50,000 epochs, followed by the LBFGS optimization.
While state-of-the-art deep learning techniques could minimize relative errors below ( 10^{-3} ) to ( 10^{-4} ) for fixed parameters, transferring these pre-trained models to new growth rates or initial values revealed significant deviations in predictions—highlighting the limitations of traditional PINNs’ generalization capabilities.
In stark contrast, our cd-PINN model successfully tackles this issue by incorporating continuous dependence on the growth rate ( r ) and initial population size ( u_0 ). Even with a single training data point, cd-PINN maintained accurate predictions across a vast parameter space, demonstrating absolute errors below ( 10^{-1} ) and often below ( 10^{-3} ). Visual comparisons revealed cd-PINN’s superior predictive performance over traditional PINN, especially in terms of absolute error distributions across parameter spaces.
The Lotka-Volterra Model
Next, we investigate the Lotka-Volterra (LV) model, which encapsulates the dynamics of two interacting species—predators and prey—governed by coupled ordinary differential equations:
[
\begin{align}
\frac{dX}{dt} &= c{11}X + c{12}XY + c{13}X^2, \
\frac{dY}{dt} &= c{21}Y + c{22}XY + c{23}Y^2, \
X(0) &= X_0, \
Y(0) &= Y_0.
\end{align}
]
The LV model exhibits various equilibrium points characterized by the Jacobian matrix. In our experiments, we designed three scenarios, with the first scenario focusing on the instability at point (0, 0) and stability at two other points, aimed to evaluate the model’s capacity to learn accurate solutions given initial values spanning different stable domains.
Real data from initial settings ( X_0 = 8.0, Y_0 = 1.0 ), combined with 214 residual data points, formed our training dataset, while testing included a range of initial values. The results revealed cd-PINN’s impressive ability to generalize, with absolute errors consistently less than ( 10^{-2} ) across broad initial conditions. Moreover, the MSE of cd-PINN showed significantly quicker convergence compared to standard PINN.
Damped Harmonic Oscillator
The dynamics of a damped harmonic oscillator provide another rich area for exploration. The governing second-order differential equation models oscillatory motion and is given by:
[
\frac{{d}^{2}x}{dt^{2}} + 2\zeta \omega_0 \frac{dx}{dt} + \omega_0^{2}x = 0
]
where ( \zeta ) indicates the damping ratio and ( \omega_0 ) is the intrinsic frequency. We explored cases of underdamped, critically damped, and overdamped systems. For each case, training involved distinct configurations while testing stretched across broader parameter spaces.
Numerical results indicated heightened accuracy of cd-PINN, notably in underdamped and critically damped conditions, where it substantially outperformed traditional algorithms that did not incorporate the continuous dependence.
Multiscale Model for p53 Activation
To test cd-PINN’s applicability in complex biological systems, we examined a multiscale model for p53 activation linked to cancer biology. This complex system utilizes multiple coupled ODEs representing gene interactions. Our test cases spanned a diverse parameter space of [(S)], [(ARF)] values, reflecting real-time dynamics of these pivotal genes.
The findings demonstrated that cd-PINN not only achieved statistically significant reductions in MSE but also effectively modeled responses to perturbations regarding gene interactions—showcasing its robustness in high-dimensional biological systems.
The Lorenz System
The sensitive nature of the Lorenz system presents a challenge for modeling chaotic behavior, where minute initial condition variances lead to drastically different outcomes. We employed a discrete-time state transition framework for cd-PINN, allowing for the effective capture of complex dynamics.
Training involved trajectories generated from varying initial conditions while employing physics-informed constraints to enhance predictive capabilities. Despite traditional approaches struggling with accuracy, cd-PINN achieved significantly lower total errors, exemplifying its proficiency in chaotic regimes.
Extension to Partial Differential Equations
The framework of cd-PINN extends beyond ODEs to complex systems governed by partial differential equations (PDEs). Employing the 2D wave equation as a concrete example, we demonstrated cd-PINN’s ability to infer solutions using parameterized conditions effectively and efficiently.
Our experiments revealed that cd-PINN outperformed several mainstream operator learning frameworks, leveraging synthesized data over extensive parameter regions, thereby emphasizing its generalizability.
Fixed Initial Values and Boundary Labeling
To further scrutinize the robustness of cd-PINN, we evaluated scenarios with fixed initial values, comparing its performance against standard PINN within the LV system. The results showcased enhanced convergence rates and prediction accuracy for cd-PINN, even when compared to strict data-regression models.
We also examined the implications of training data positioning at the domain boundary. While training near boundaries produced slight increases in absolute error compared to central-domain training, it still remained within acceptable limits.
Hyperparameter Influence and Computation Cost
Analyzing the influence of hyperparameters on model performance revealed balancing acts necessary for optimizing convergence rates and prediction accuracy. Variations in the weighting term for the continuous dependence loss impacted training stability, modeling efficiency, and resultant accuracy.
Moreover, we presented a comparative examination of computational costs against traditional ODE solvers, highlighting cd-PINN’s advantageous scalability and speed, allowing it to manage vast parameter spaces efficiently.
Comparison with Neural ODEs and Conventional Solvers
Through numerical experiments, we highlighted the advantages of cd-PINN over Neural ODEs, demonstrating not only superior generalization capabilities but also enhanced computational efficiency—performing significantly faster even in complex dynamical systems.
Lastly, the distinct strengths of cd-PINN over conventional numerical solvers underscore its potential to revolutionize the field of ODE resolution, offering real-time solutions across expansive parameter spaces with accuracy and speed previously unattainable.