Understanding the Interleaved Physics-Based Deep-Learning Framework for Microstructurally Small Crack Growth Prediction

Recent advancements in predicting the growth of microstructurally small cracks (MSCs) have been accelerated by the integration of deep learning and physics-based methods. A notable study highlighted that trained Bidirectional Long Short-Term Memory (BiLSTM) models are adept at mapping crack growth parameters by harnessing microstructural and micromechanical features extracted from the uncracked areas of the simulation. This intersection of machine learning with physics-based simulations promises more accurate predictions, as the microstructure remains static during crack propagation, making micromechanical features the primary drivers of accuracy.

The Interleaved Physics-Based Deep-Learning Framework

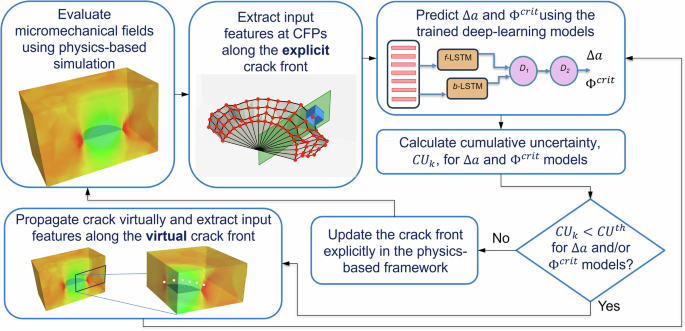
Innovative in its approach, the interleaved Physics-Based Deep-Learning (PBDL) framework seamlessly merges the strengths of both deep learning and physics-based simulations. Figure 1 showcases the prediction process, beginning with micromechanical evaluations in a physics-based framework that incorporates an initial crack within the finite element (FE) mesh. Following this, input sequences are generated at various crack front points (CFPs). The trained BiLSTM models then predict parameters such as local crack extension (Δa) and critical kink angle (Φ^crit) for each CFP, while also providing uncertainty estimates for their predictions.

This framework operates on the premise that predictions are considered valid only if model uncertainty falls beneath a user-defined threshold. If so, these predictions facilitate the virtual propagation of the crack from state k=0 to k=1. As crack evolution progresses, new sequences are gathered from the updated crack front, continuing the predictive cycle. However, it’s essential to note that as the crack moves away from its initiation point, the relevance of earlier micromechanical fields diminishes, leading to accruing errors and uncertainties over time.

When the cumulative uncertainty exceeds a set threshold, the prediction paradigm shifts back to physics-based simulations. A new representation of the crack surface in the FE mesh allows for an accurate update of micromechanical fields, re-establishing fidelity in predictive capabilities. The predictions resume with these updated features, effectively leveraging both methodologies.

Demonstrating the Interleaved PBDL Framework

To showcase the potential of the interleaved PBDL framework, researchers conducted experiments with microstructural instantiations from a comprehensive test dataset. The objective was to analyze how errors and computational expenses varied while propagating a crack from k=0 to k=7, utilizing three distinct methodologies: traditional physics-based simulations, a deep-learning-only method, and the interleaved PBDL framework.

Figure 2 illustrates incremental crack surface evolution alongside associated micromechanical fields, comparing the three frameworks. The analysis draws attention to the importance of cumulative uncertainty thresholds, such as T₁=0.8 μm and T₂=0.4 μm. These strategically chosen thresholds govern the frequency of updates to the physics-based models, revealing a clear trend: as uncertainty thresholds tighten, predictions improve in accuracy.

In the deep-learning-only case, the models often relied on outdated micromechanical fields, ultimately leading to significant discrepancies compared to physics-based predictions. In contrast, the interleaved PBDL framework maintained more robust predictability due to its adaptive reliance on updated fields.

Error Dynamics in Crack Propagation

An important aspect of studying MSC growth is understanding the error dynamics as the crack advances. The study highlighted that while uncertainty resets with every physics-based update, overall error continues to compound as the crack propagates. This is especially pertinent in MSCs, which evolve as complex, tortuous 3D surfaces. As such, researchers measured the primary error metric by comparing the predicted crack surface area against high-fidelity physics-based simulations.

Figure 3 depicts error trends of total crack surface area relative to average crack radius. The results illustrate a polynomial relationship where the interleaved PBDL framework demonstrated superior control over error growth compared to the deep-learning-only method. Notably, tighter cumulative uncertainty thresholds led to reduced error, emphasizing the effectiveness of frequent updates when predicting crack trajectories.

While initial discrepancies between prediction methods may seem minor, they can escalate dramatically. In instances where predictions were solely reliant on deep learning, the error escalated to approximately 318% of the actual average crack radius. On the contrary, the interleaved PBDL framework limited error accumulation more effectively, maintaining deviations to around 41% and 29% for thresholds T₁ and T₂, respectively.

Computational Efficiency of the PBDL Framework

In considering both accuracy and computational efficiency, the interleaved PBDL framework stands out as a pragmatic solution for predicting crack evolution. Figure 4 illustrates projected computational costs associated with the three methodologies. While the interleaved PBDL framework was found to be more computationally intensive than the deep-learning-only approach, it still offered a substantial reduction in costs compared to traditional physics-based simulations—reducing expenses by a factor of three to four, depending on the chosen uncertainty thresholds.

This highlights a crucial trade-off; while more computational resources may be expended, the overall efficiency gained through an adaptive model ensures that engineers and researchers can make informed decisions on crack propagation without incurring excessive costs or delays.

With the ongoing evolution of deep learning and physics-based frameworks, the interleaved PBDL model represents an innovative synthesis of these approaches, setting a benchmark for future research and applications in the field of material science and structural integrity.