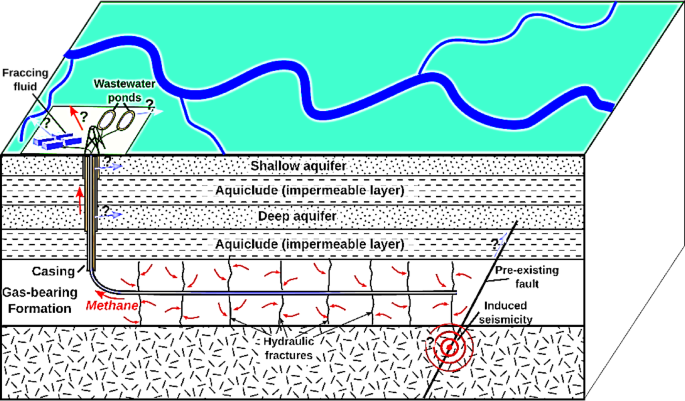
Peculiarities of the Applied Machine Learning Methods in Hydraulic Fracturing Analysis
In the realm of hydraulic fracturing (HF) analysis, the application of machine learning (ML) methods has been revolutionized by a unique framework that stands apart from traditional approaches. This article delves into the distinctive features of this framework, elucidating its robustness and its ability to capture intricate relationships among various parameters in HF.
Utilizing a Large-Scale Dataset
One of the hallmark features of this study is the use of a large-scale dataset consisting of 16,000 records. This dataset far exceeds the sizes commonly employed in previous studies, thereby enhancing the robustness and generalizability of the predictive models. By leveraging a dataset of this magnitude, the models are better equipped to delineate the underlying patterns and interactions among HF parameters, which are critical for accurate predictions.
Comprehensive Statistical Analysis
Another noteworthy aspect of this methodology is the thorough integration of comprehensive statistical analyses. By evaluating metrics such as mean, variance, skewness, kurtosis, and quartiles, and employing data visualization techniques such as box plots and violin plots, the study provides a nuanced understanding of the distribution and variability of input variables. This detailed preprocessing is crucial, as it lays the groundwork for improved model accuracy and interpretability—a step often overlooked in many data-driven HF studies.
For instance, summarizing the statistical characteristics of input variables enables researchers to pinpoint trends and anomalies in the data. This understanding is vital in HF, where even minor variations can significantly impact outcomes.
Systematic Evaluation of Model Performance
A unique methodology in this study includes an evaluation of model performance across a range of train/test ratios (0.1 to 0.9). This systematic approach allows researchers to assess how variations in data availability influence model performance and stability. By analyzing the R² values across these splits and supporting the findings with multiple independent runs for each model, insights into the reliability and consistency of different ML algorithms under diverse data constraints are garnered.
Incorporation of Domain-Specific Parameters
What sets this framework apart further is the deliberate inclusion of domain-specific parameters, such as fracture height, fracture length, fluid viscosity, and injection time. These parameters, directly derived from the governing physical equations of HF, ensure that the ML models remain relevant to real-world operations. The integration of physics-based variables makes the models not only data-driven but also closely aligned with conventional engineering principles, which is a critical advantage in the field.
Comparative Evaluation of Algorithms
Additionally, this study employs a fair comparative framework by evaluating three well-established algorithms—Random Forest (RF), Neural Networks (NN), and Support Vector Machines (SVM)—under uniform conditions. The findings revealed that RF outperformed the others in terms of accuracy and error minimization, showcasing its efficacy for HF analysis.
Data Preprocessing and Initial Analysis
The data preprocessing stage involves using MATLAB libraries to implement SVM, NN, and RF methods. Microsoft Excel is utilized for organizing and sorting datasets, underscoring the accessibility of these powerful ML tools. The analysis commences with plotting data using analytical formulas, followed by assessing patterns pivotal to the modeling process. This step is crucial as it clears the path for meaningful application of the chosen ML algorithms.
For the HF process, four critical parameters are analyzed, represented by specific symbols: viscosity of the fracturing fluid (µ, in centipoise), height of the fracture (h), injection time (t), and length of the fracture (X). Each metric provides foundational insights essential for developing predictive models and strategies.
The significance of understanding parameter interrelationships becomes especially evident in HF, where the interplay between fluid flow and fracture propagation significantly shapes outcomes.
Statistical Insights and Visualizations
Employing several key statistical metrics, the distribution characteristics of HF parameters are systematically presented. The analyses provided through graphical representations such as box plots serve to visualize a spectrum of indicators, including the median, quartiles, and variance. For instance, the median effectively splits datasets into two equal halves, minimizing the impact of potential outliers. Variance analysis elucidates how different parameters spread out, offering valuable assessments for model tuning and reliability checks.
Box plots and violin plots (as illustrated in Figure 3) further enhance understanding by visualizing statistical indicators, clarifying the distribution of various HF parameters.
Data Characteristics
Through statistical evaluations of viscosity, fracture height, fracture length, and injection time, substantial variability is apparent. Viscosity, for instance, ranges dramatically from 50.437 to 999.798 centipoise, underscoring its critical role in the HF process. Such insights into median and quartile values offer a cohesive understanding of the data while reinforcing the model’s predictive capabilities.
Correlation Analysis
Utilizing a correlation matrix as shown in Figure 4, the interrelationships among the variables are revealed. With coefficients nearing +1 indicating strong positive correlations and those hovering around zero suggesting limited relationships, this analysis becomes instrumental in identifying critical factors that drive HF performance.
Implementing Machine Learning Methods
Neural Networks (NN)
Neural networks mirror the structure and operational principles of the human brain. Comprising interconnected nodes, these networks excel in addressing complex problems across various fields, including image recognition. Each NN includes three core layer types: input, hidden, and output layers, with data flowing through weighted connections. The training process revolves around adjusting these weights to minimize prediction errors, enabling the NN to learn and adapt.
Random Forest (RF)
Random Forest algorithm utilizes an ensemble learning approach, amalgamating multiple decision trees to enhance model accuracy and mitigate overfitting. This methodology employs Bootstrap Aggregation (Bagging) to generate diverse training subsets for each tree, thus ensuring varied and robust decision-making. The aggregation results in predictions characterized by both majority voting for classification and averaged outputs for regression tasks, delivering high accuracy and resilience against data fluctuations.
Support Vector Machines (SVM)
SVM operates by finding an optimal hyperplane to segregate diverse classes while maximizing the margin between them. This separation process is enhanced by employing kernel functions to address non-linear challenges, enabling the SVM to function effectively in higher-dimensional spaces. The framework incorporates slack variables to handle misclassifications, allowing SVM to balance between a wide margin and minimized errors.
Convergence of Machine Learning and Hydraulic Fracturing
The integration of ML algorithms into HF analysis is not merely a technological upgrade but a paradigm shift. With applications ranging from predicting reservoir characteristics to optimizing extraction processes, ML showcases its potential to redefine operational efficiency in the oil and gas industry.
Recent studies, such as those by Kamali et al. and Ghorbani et al., highlight the successful adoption of ML models in predicting hydraulic fracturing outcomes. These advancements not only signify progress in analytical methodologies but also reinforce the profound implications of machine learning within complex and dynamic operational landscapes.
Through this study’s unique approach, the fusion of robust data analytics with domain-specific insights and advanced machine learning methods results in a more effective framework to address the challenges posed in hydraulic fracturing analysis. The exploration of this intersection lays the foundation for future research and optimization strategies, ultimately contributing to improved production outcomes in the hydraulic fracturing domain.